如图,在边长为1的正方形 中, 是边 的中点,点 是边 上一点(与点 、 不重合),射线 与 的延长线交于点 .
(1)求证: ;
(2)过点 作 交 于点 ,连接 ,当 时,
①求证:四边形 是平行四边形;
②请判断四边形 是否为菱形,并说明理由.

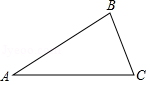
如图,在△ ABC中,内角 A、 B、 C所对的边分别为 a、 b、 c.
(1)若 a=6, b=8, c=12,请直接写出∠ A与∠ B的和与∠ C的大小关系;
(2)求证:△ ABC的内角和等于180°;
(3)若 ,求证:△ ABC是直角三角形.
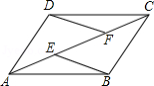
已知:如图, 、 是平行四边形 的对角线 上的两点, .
求证:(1) ;
(2) .
如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.

问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图,四边形 为平行四边形,连接 ,且 .请用尺规完成基本作图:作出 的角平分线与 交于点 .连接 交 于点 ,交 于点 ,猜想线段 和线段 的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作法)

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

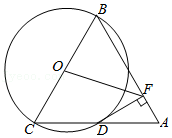
如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

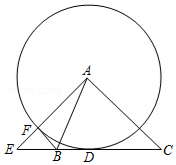
如图,以等边三角形 的 边为直径画圆,交 于点 , 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)求线段 的长度.
如图,在 中, , , , ,点 是边 上一点,连接 ,将 沿 翻折得到 .
(1)若 , ,且 ,求 的长;
(2)连接 ,若四边形 是平行四边形,求 与 之间的关系式.

如图,在 中, ,点 、 分别在 、 上, , 、 相交于点 .
(1)求证: ;
(2)求证: .
