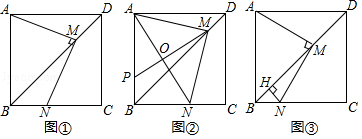
如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.
相关知识点
推荐套卷
如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.
