小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:
(1)绘制函数图象
①列表:如表是 与 的几组对应值,其中 ;
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
②描点:根据表中的数值描点 ,请补充描出点 ;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
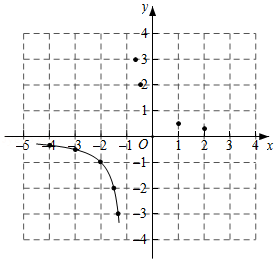
(2)探究函数性质
判断下列说法是否正确(正确的填“ ”,错误的填“ ”
①函数值 随 的增大而减小: .
②函数图象关于原点对称: .
③ 函数图象与直线 没有交点: .
如图,反比例函数 的图象与一次函数 的图象相交于 , 两点.
(1)求反比例函数和一次函数的解析式;
(2)设直线 交 轴于点 ,点 是 轴正半轴上的一个动点,过点 作 轴交反比例函数 的图象于点 ,连接 , .若 ,求 的取值范围.

阅读理解:
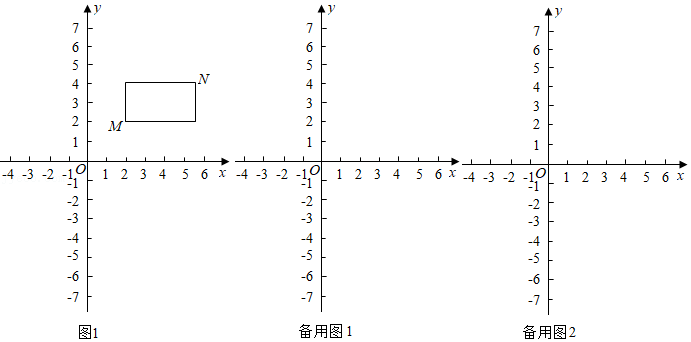
在平面直角坐标系中,点 的坐标为 , ,点 的坐标为 , ,且 , ,若 、 为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为 、 的"相关矩形".如图1中的矩形为点 、 的"相关矩形".
(1)已知点 的坐标为 .
①若点 的坐标为 ,则点 、 的"相关矩形"的周长为 ;
②若点 在直线 上,且点 、 的"相关矩形"为正方形,求直线 的解析式;
(2)已知点 的坐标为 ,点 的坐标为 若使函数 的图象与点 、 的"相关矩形"有两个公共点,直接写出 的取值.
如图, 中, ,顶点 , 都在反比例函数 的图象上,直线 轴,垂足为 ,连结 , ,并延长 交 于点 ,当 时,点 恰为 的中点,若 , .
(1)求反比例函数的解析式;
(2)求 的度数.

如图,正比例函数 与反比例函数 的图象交于点 ,过点 作 轴于点 , ,点 在线段 上,且 .
(1)求 的值及线段 的长;
(2)点 为 点上方 轴上一点,当 与 的面积相等时,请求出点 的坐标.

已知反比例函数 的图象经过点 .
(1)求该反比例函数的表达式;
(2)如图,在反比例函数 的图象上点 的右侧取点 ,过点 作 轴的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 .
①过点 ,点 分别作 轴, 轴的垂线,两线相交于点 ,求证: , , 三点共线;
②若 ,求证: .
如图,在平面直角坐标系中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.

如图,四边形 的四个顶点分别在反比例函数 与 的图象上,对角线 轴,且 于点 .已知点 的横坐标为4.
(1)当 , 时.
①若点 的纵坐标为2,求直线 的函数表达式.
②若点 是 的中点,试判断四边形 的形状,并说明理由.
(2)四边形 能否成为正方形?若能,求此时 , 之间的数量关系;若不能,试说明理由.

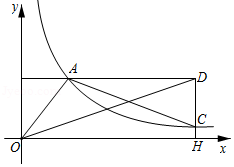
如图,过 点的直线 与 轴, 轴分别交于点 , 两点,且 ,过点 作 轴,垂足为点 ,交反比例函数 的图象于点 ,连接 , 的面积为6.
(1)求 值和点 的坐标;
(2)如图,连接 , ,点 在直线 上,且位于第二象限内,若 的面积是 面积的2倍,求点 的坐标.

如图,一次函数 与反比例函数 的图象交于点 , .
(1)求反比例函数和一次函数的解析式;
(2)判断点 是否在一次函数 的图象上,并说明理由;
(3)写出不等式 的解集.

如图,在平面直角坐标系中, 点的坐标为 , 轴于点 , ,反比例函数 的图象的一支分别交 、 于点 、 .延长 交反比例函数的图象的另一支于点 .已知点 的纵坐标为 .
(1)求反比例函数的解析式;
(2)求直线 的解析式;
(3)求 .

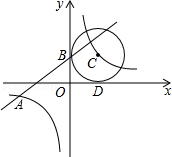
如图,已知一次函数 的图象与反比例函数 的图象交于点 ,且与 轴交于点 ,第一象限内点 在反比例函数 的图象上,且以点 为圆心的圆与 轴, 轴分别相切于点 ,
(1)求 的值;
(2)求一次函数的表达式;
(3)根据图象,当 时,写出 的取值范围.
如图, 中, , ,点 ,点 ,反比例函数 的图象经过点 .
(1)求反比例函数的解析式;
(2)将直线 向上平移 个单位后经过反比例函数 图象上的点 ,求 , 的值.

设函数 , .
(1)当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.
(2)设 ,且 ,当 时, ;当 时, .圆圆说:“ 一定大于 ”.你认为圆圆的说法正确吗?为什么?
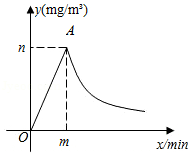
为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要 ;完成2间办公室和1间教室的药物喷洒要 .
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度 (单位: 与时间 (单位: 的函数关系如图所示:校医进行药物喷洒时 与 的函数关系式为 ,药物喷洒完成后 与 成反比例函数关系,两个函数图象的交点为 .当教室空气中的药物浓度不高于 时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.