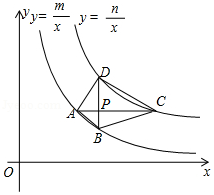
如图，四边形 的四个顶点分别在反比例函数 与 的图象上，对角线 轴，且 于点 ．已知点 的横坐标为4．
（1）当 ， 时．
①若点 的纵坐标为2，求直线 的函数表达式．
②若点 是 的中点，试判断四边形 的形状，并说明理由．
（2）四边形 能否成为正方形？若能，求此时 ， 之间的数量关系；若不能，试说明理由．
相关试题
“初中生骑电动车上学”的现象越来越受到社会的关注，某校利用“五一”假期，随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法，统计整理制作了如下的统计图，请回答下列问题：
⑴这次共抽查了个家长；
⑵请补全条形统计图和扇形统计图（友情提醒：条形图补画家长持“反对”态度的人数条，扇形图填上“反对”及“赞成”的百分数）；
⑶已知该校共有1200名学生，持“赞成”态度的学生估计约有人．
ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．求证：BE=DF．
（2）解不等式组：
（2）化简
．如图，在平面直角坐标系中，点A坐标为(-2，0)，点B坐标为（0，2），点E为线段AB上的动点(点E不与点A，B重合)，以E为顶点作∠OET=45°，射线ET交线段OB于点F，C为y轴正半轴上一点，且OC=AB，抛物线y=
x2+mx+n的图象经过A，C两点.
（1）求此抛物线的函数表达式；
（2）求证：∠BEF=∠AOE；
（3）当△EOF为等腰三角形时，求此时点E的坐标；
（4）在（3）的条件下，当直线EF交x轴于点D，P为（1）中抛物线上一动点，直线PE交x轴于点G，在直线EF上方的抛物线上是否存在一点P，使得△EPF的面积是△EDG面积的（
）倍.若存在，请直接写出点P坐标；若不存在，请说明理由．
推荐套卷
粤公网安备 44130202000953号