(本题8分)某商场销售某种品牌的纯牛奶,已知进价为每箱40元,市场调查发现,若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多售3箱,价格每升高1元,平均每天少售3箱。
①写出平均每天的销售量y与每箱售价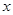 之间关系;
之间关系;
②求出商场平均每天销售这种牛奶的利润w与每箱售价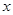 之间的关系;
之间的关系;
③求在的情况下当牛奶每箱售价定为多少时可达到最大利润,最大利润是多少元?
相关知识点
推荐套卷
(本题8分)某商场销售某种品牌的纯牛奶,已知进价为每箱40元,市场调查发现,若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多售3箱,价格每升高1元,平均每天少售3箱。
①写出平均每天的销售量y与每箱售价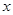 之间关系;
之间关系;
②求出商场平均每天销售这种牛奶的利润w与每箱售价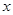 之间的关系;
之间的关系;
③求在的情况下当牛奶每箱售价定为多少时可达到最大利润,最大利润是多少元?