如图1，直线l1：y=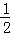
x+1与l2：y=﹣2x+6相交于点C，直线l1分别与x轴、y轴相交于点A、D，直线l2分别与x轴、y轴交于点B、E．
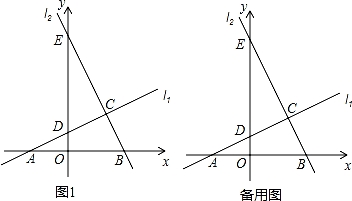
（1）填空：①线段AB= ；②点C的坐标为 ；
（2）求证：△ABC是直角三角形；
（3）直线l1向上平移几个单位后，以点A、B、E、D为顶点的图形是轴对称图形？（直接写出答案）
）2-（
）2．相关知识点
推荐套卷
如图1，直线l1：y=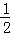x+1与l2：y=﹣2x+6相交于点C，直线l1分别与x轴、y轴相交于点A、D，直线l2分别与x轴、y轴交于点B、E．
（1）填空：①线段AB= ；②点C的坐标为 ；
（2）求证：△ABC是直角三角形；
（3）直线l1向上平移几个单位后，以点A、B、E、D为顶点的图形是轴对称图形？（直接写出答案）
粤公网安备 44130202000953号