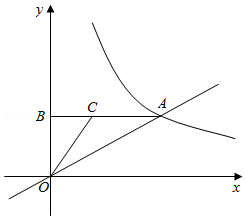
如图,正比例函数 与反比例函数 的图象交于点 ,过点 作 轴于点 , ,点 在线段 上,且 .
(1)求 的值及线段 的长;
(2)点 为 点上方 轴上一点,当 与 的面积相等时,请求出点 的坐标.
相关知识点
推荐套卷
如图,正比例函数 与反比例函数 的图象交于点 ,过点 作 轴于点 , ,点 在线段 上,且 .
(1)求 的值及线段 的长;
(2)点 为 点上方 轴上一点,当 与 的面积相等时,请求出点 的坐标.
