阅读理解：
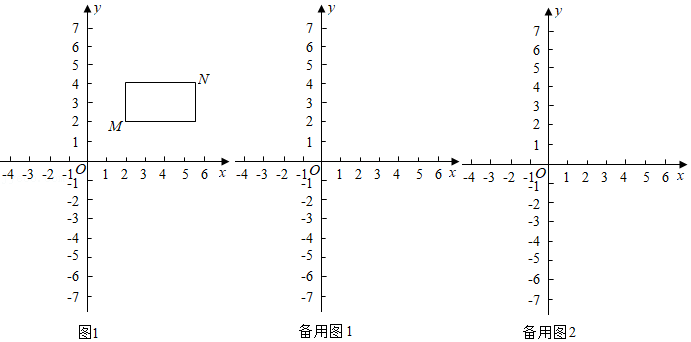
在平面直角坐标系中，点 的坐标为 ， ，点 的坐标为 ， ，且 ， ，若 、 为某矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为 、 的"相关矩形"．如图1中的矩形为点 、 的"相关矩形"．
（1）已知点 的坐标为 ．
①若点 的坐标为 ，则点 、 的"相关矩形"的周长为 ；
②若点 在直线 上，且点 、 的"相关矩形"为正方形，求直线 的解析式；
（2）已知点 的坐标为 ，点 的坐标为 若使函数 的图象与点 、 的"相关矩形"有两个公共点，直接写出 的取值．
数学兴趣小组成员张明对本班期末考试数学成绩(成绩取整数，满分为100分)作了统计分析，绘制成如下频数、频率分布表和频数分布直方图．请你根据图表提供的信息，解答下列问题：
| 分组 |
49.5~59.5 |
59.5~69.5 |
69.5~79.5 |
79.5~89.5 |
89.5~100.5 |
合计 |
| 频数 |
2 |
a |
20 |
16 |
4 |
50 |
| 频率 |
0.04 |
0.16 |
0.40 |
0.32 |
b |
1 |
（1）频数、频率分布表中a=，b=；
（2）补全频数分布直方图；
（3）数学老师准备从不低于90分的学生中选1人介绍学习经验，那么取得了94分的张明被选上的概率是多少？
已知△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D为BC边上一点．
（1）求证：△ACE≌△ABD；
（2）若AC=2
，CD=1，求ED的长．
如图，直线
与x轴正半轴交于点A（2，0），以OA为边在x轴上方作正方形OABC，延长CB交直线
于点D，再以BD为边向上作正方形BDEF．
（1）求点F的坐标；
（2）设直线OF的解析式为
，若
，求x的取值范围．
自古以来，钓鱼岛及其附属岛屿都是我国固有领土。如图，为了开发利用海洋资源，我勘测飞机测量钓鱼岛附属岛屿之一的北小岛（又称为鸟岛）两侧端点A、B的距离，飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了800米，在点D测得端点B的俯角为45°，求北小岛两侧端点A、B的距离.
（结果精确到0.1米，参考数据
）
粤公网安备 44130202000953号