初中数学一元二次方程解答题

已知关于 $x$的一元二次方程 $x^2+x-m=0$．

（1）若方程有两个不相等的实数根，求 $m$的取值范围；

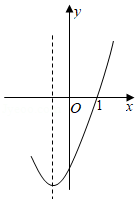
（2）二次函数 $y=x^2+x-m$的部分图象如图所示，求一元二次方程 $x^2+x-m=0$的解．

已知关于 $x$的一元二次方程： $x^2-2x-k-2=0$有两个不相等的实数根．

（1）求 $k$的取值范围；

（2）给 $k$取一个负整数值，解这个方程．

已知关于 $x$的一元二次方程 $m{x}^2+(1-5m)x-5=0(m\ne 0)$．

（1）求证：无论 $m$为任何非零实数，此方程总有两个实数根；

（2）若抛物线 $y=m{x}^2+(1-5m)x-5$与 $x$轴交于 $A(x_1$， $0)$、 $B(x_2$， $0)$两点，且 $|x_1-x_2|=6$，求 $m$的值；

（3）若 $m>0$，点 $P(a,b)$与 $Q(a+n,b)$在（2）中的抛物线上（点 $P$、 $Q$不重合），求代数式 $4a^2-n^2+8n$的值．

今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；

（2）若该景区仅有 $A$ ， $B$ 两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	$A$	$B$	$A$ 和     $B$
门票价格	100元     $/$ 人	80元     $/$ 人	160元     $/$ 人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．

①若丙种门票价格下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

已知关于 $x$的一元二次方程 $x^2-(2k+1)x+k^2+k=0$．

（1）求证：无论 $k$取何值，方程都有两个不相等的实数根．

（2）如果方程的两个实数根为 $x_1$， $x_2$，且 $k$与 $\frac{x_1}{x_2}$都为整数，求 $k$所有可能的值．

若三个非零实数 $x$， $y$， $z$满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数 $x$， $y$， $z$构成“和谐三组数”．

（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；

（2）若 $M(t,y_1)$， $N(t+1,y_2)$， $R(t+3,y_3)$三点均在函数 $y=\frac{k}{x}(k$为常数， $k\ne 0)$的图象上，且这三点的纵坐标 $y_1$， $y_2$， $y_3$构成“和谐三组数”，求实数 $t$的值；

（3）若直线 $y=2\mathit{bx}+2c(\mathit{bc}\ne 0)$与 $x$轴交于点 $A(x_1$， $0)$，与抛物线 $y=a{x}^2+3\mathit{bx}+3c(a\ne 0)$交于 $B(x_2$， $y_2)$， $C(x_3$， $y_3)$两点．

①求证： $A$， $B$， $C$三点的横坐标 $x_1$， $x_2$， $x_3$构成“和谐三组数”；

②若 $a>2b>3c$， $x_2=1$，求点 $P(\frac{c}{a}$， $\frac{b}{a})$与原点 $O$的距离 $\mathit{OP}$的取值范围．

根据衢州市统计局发布的统计数据显示，衢州市近5年国民生产总值数据如图1所示，2016年国民生产总值中第一产业，第二产业，第三产业所占比例如图2所示．

请根据图中信息，解答下列问题：

（1）求2016年第一产业生产总值（精确到1亿元）

（2）2016年比2015年的国民生产总值增加了百分之几？（精确到 $1\%)$

（3）若要使2018年的国民生产总值达到1573亿元，求2016年至2018年我市国民生产总值的平均增长率（精确到 $1\%)$

为进一步促进义务教育均衡发展，某市加大了基础教育经费的投入，已知2015年该市投入基础教育经费5000万元，2017年投入基础教育经费7200万元．

（1）求该市这两年投入基础教育经费的年平均增长率；

（2）如果按（1）中基础教育经费投入的年平均增长率计算，该市计划2018年用不超过当年基础教育经费的 $5\%$购买电脑和实物投影仪共1500台，调配给农村学校，若购买一台电脑需3500元，购买一台实物投影需2000元，则最多可购买电脑多少台？

某烘焙店生产的蛋糕礼盒分为六个档次，第一档次（即最低档次）的产品每天生产76件，每件利润10元．调查表明：生产每提高一个档次的蛋糕产品，该产品每件利润增加2元．

（1）若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；

（2）由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？

我们规定：若 $\vec{m}=(a,b)$， $\vec{n}=(c,d)$，则 $\vec{m}·\vec{n}=\mathit{ac}+\mathit{bd}$．如 $\vec{m}=(1,2)$， $\vec{n}=(3,5)$，则 $\vec{m}·\vec{n}=1\times 3+2\times 5=13$．

（1）已知 $\vec{m}=(2,4)$， $\vec{n}=(2,-3)$，求 $\vec{m}·\vec{n}$；

（2）已知 $\vec{m}=(x-a,1)$， $\vec{n}=(x-a,x+1)$，求 $y=\vec{m}·\vec{n}$，问 $y=\vec{m}·\vec{n}$的函数图象与一次函数 $y=x-1$的图象是否相交，请说明理由．

由多项式乘法： $(x+a)(x+b)=x^2+(a+b)x+\mathit{ab}$，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式： $x^2+(a+b)x+\mathit{ab}=(x+a)(x+b)$．

示例：分解因式： $x^2+5x+6=x^2+(2+3)x+2\times 3=(x+2)(x+3)$．

（1）尝试：分解因式： $x^2+6x+8=(x+$　　 $\left)\right(x+$　　 $)$；

（2）应用：请用上述方法解方程： $x^2-3x-4=0$．

在面积都相等的所有矩形中，当其中一个矩形的一边长为1时，它的另一边长为3．

（1）设矩形的相邻两边长分别为 $x$， $y$．

①求 $y$关于 $x$的函数表达式；

②当 $y⩾3$时，求 $x$的取值范围；

（2）圆圆说其中有一个矩形的周长为6，方方说有一个矩形的周长为10，你认为圆圆和方方的说法对吗？为什么？

收发微信红包已成为各类人群进行交流联系、增强感情的一部分，下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话．

请问：（1）2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少？

（2）2017年六一甜甜和她妹妹各收到了多少钱的微信红包？

某种商品的标价为400元/件，经过两次降价后的价格为324元/件，并且两次降价的百分率相同．

（1）求该种商品每次降价的百分率；

（2）若该种商品进价为300元/件，两次降价共售出此种商品100件，为使两次降价销售的总利润不少于3120元．问第一次降价后至少要售出该种商品多少件？

已知关于x的方程 $x^2\mathit{﹣（}2m+1）x+m（m+1\mathit{）＝}0$．

（1）求证：方程总有两个不相等的实数根；

（2）已知方程的一个根为 $x＝0$，求代数式 $（2m﹣1{）}^2+（3+m\mathit{）（}3﹣m）+7m﹣5$的值（要求先化简再求值）．