为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2015年该市投入基础教育经费5000万元,2017年投入基础教育经费7200万元.
(1)求该市这两年投入基础教育经费的年平均增长率;
(2)如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2018年用不超过当年基础教育经费的 购买电脑和实物投影仪共1500台,调配给农村学校,若购买一台电脑需3500元,购买一台实物投影需2000元,则最多可购买电脑多少台?
相关知识点
推荐套卷
 )
)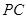 是⊙
是⊙ 的切线;
的切线; ,
, 时,求PC的长.
时,求PC的长.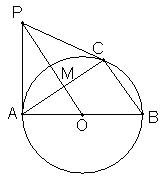

 米;
米; ).
).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号