如图,在以为直角顶点的等腰直角三角形纸片
中,将
角折起,使点
落在
边上的点
(不与点
,
重合)处,折痕是
.

如图1,当时,
;
如图2,当时,
;
如图3,当时,
;
依此类推,当为正整数)时,
.
南宋数学家杨辉在其著作《详解九章算法》中揭示了 为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为"杨辉三角"
则 展开式中所有项的系数和是

| A. |
128 |
B. |
256 |
C. |
512 |
D. |
1024 |
数轴上,
两点的距离为4,一动点
从点
出发,按以下规律跳动:第1次跳动到
的中点
处,第2次从
点跳动到
的中点
处,第3次从
点跳动到
的中点
处,按照这样的规律继续跳动到点
,
,
,
,
.
,
是整数)处,那么线段
的长度为 .

已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 , 的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数 依此类推,那么 的值是
| A. |
|
B. |
7.5 |
C. |
5.5 |
D. |
|
观察下列一组数:
,
,
,
,
,
,
它们是按一定规律排列的,请利用其中规律,写出第个数
(用含
的式子表示)
阅读下列材料:小明为了计算的值,采用以下方法:
设①
则②
②①得
请仿照小明的方法解决以下问题:
(1)
;
(2) ;
(3)求的和
,
是正整数,请写出计算过程).
如图,过点 作 轴的垂线交直线 于点 ,过点 作直线 的垂线,交 轴于点 ,过点 作 轴的垂线交直线 于点 , ,这样依次下去,得到△ ,△ ,△ , ,其面积分别记为 , , , ,则 为
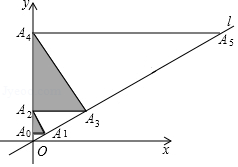
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中,点
,
、
,
、
,
,
,
,
均在反比例函数
的图象上,点
、
、
、
、
均在
轴的正半轴上,且△
、△
、△
、
、△
均为等腰直角三角形,
、
、
、
、
分别为以上等腰直角三角形的底边,则
的值等于 .
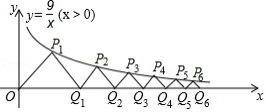
是不为1的有理数,我们把 称为 的差倒数,如2的差倒数为 , 的差倒数 ,已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数 ,依此类推, 的值是
| A. |
5 |
B. |
|
C. |
|
D. |
|
我国的《洛书》中记载着世界上最古老的一个幻方:将这九个数字填入
的方格内,使三行、三列、两对角线上的三个数之和都相等.如图的幻方中,字母
所表示的数是 .

在数的学习过程中,我们总会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了偶数、奇数、合数、质数等.现在我们来研究一种特殊的自然数 “纯数”.
定义:对于自然数,在通过列竖式进行
的运算时各位都不产生进位现象,则称这个自然数
为“纯数”.
例如:32是“纯数”,因为在列竖式计算时各位都不产生进位现象;23不是“纯数”,因为
在列竖式计算时个位产生了进位.
(1)请直接写出1949到2019之间的“纯数”;
(2)求出不大于100的“纯数”的个数,并说明理由.