初中数学试题

如图，BD是矩形ABCD的对角线．

（1）求作 $\odot A$，使得 $\odot A$与 $BD$相切（要求：尺规作图，不写作法，保留作图痕迹）；

（2）在（1）的条件下，设BD与 $\odot A$相切于点E， $CF\perp BD$，垂足为F．若直线CF与 $\odot A$相切于点G，求 $\tan \angle ADB$的值．

在平面直角坐标系xOy中，已知点 $M（a，b）$，N．

对于点P给出如下定义：将点P向右 $（a\ge 0）$或向左 $（a＜0）$平移 $\left|a\right|$个单位长度，再向上 $（b\ge 0）$或向下 $（b＜0）$平移 $\left|b\right|$个单位长度，得到点P′，点P′关于点N的对称点为Q，称点Q为点P的“对应点”．

（1）如图，点 $M（1，1）$，点N在线段OM的延长线上．若点 $P（﹣2，0）$，点Q为点P的“对应点”．

①在图中画出点Q；

②连接PQ，交线段ON于点T，求证： $NT=\frac{1}{2}OM$；

（2）⊙O的半径为 $1$，M是⊙O上一点，点N在线段OM上，且 $ON＝t（\frac{1}{2}＜t＜1）$，若P为⊙O外一点，点Q为点P的“对应点”，连接PQ．当点M在⊙O上运动时，直接写出PQ长的最大值与最小值的差（用含t的式子表示）．

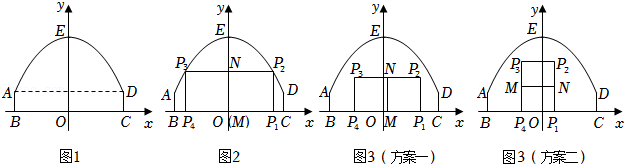
如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系 $xOy$，规定一个单位长度代表1米．E $（0，8）$是抛物线的顶点．

（1）求此抛物线对应的函数表达式；

（2）在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点 $P_1，P_4$在x轴上，MN与矩形 $P_1{P}_2{P}_3{P}_4$的一边平行且相等．栅栏总长l为图中粗线段 $P_1{P}_2，P_2{P}_3，P_3{P}_4，$MN长度之和，请解决以下问题：

（ⅰ）修建一个“”型栅栏，如图2，点 $P_2，P_3$在抛物线AED上．设点P₁的横坐标为 $m（0＜m\le 6）$，求栅栏总长l与m之间的函数表达式和l的最大值；

（ⅱ）现修建一个总长为18的栅栏，有如图3所示的“”型和“”型两种设计方案，请你从中选择一种，求出该方案下矩形 $P_1{P}_2{P}_3{P}_4$面积的最大值，及取最大值时点P₁的横坐标的取值范围（P₁在P₄右侧）．

已知二次函数图象的顶点坐标为 $A（1，4）$，且与x轴交于点 $B（﹣1，0）$．

（1）求二次函数的表达式；

（2）如图，将二次函数图象绕x轴的正半轴上一点 $P（m，0）$旋转 $180°$，此时点A、B的对应点分别为点C、D．

①连结AB、BC、CD、DA，当四边形ABCD为矩形时，求m的值；

②在①的条件下，若点M是直线x＝m上一点，原二次函数图象上是否存在一点Q，使得以点B、C、M、Q为顶点的四边形为平行四边形，若存在，求出点Q的坐标；若不存在，请说明理由．

如图，平行四边形ABCD中， $DB＝2\sqrt{3}$， $AB＝4，AD＝2，$动点E、F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．

（1）如图1，设点E的速度为1个单位每秒，点F的速度为4个单位每秒，当运动时间为 $\frac{2}{3}$秒时，设CE与DF交于点P，求线段EP与CP长度的比值；

（2）如图2，设点E的速度为1个单位每秒，点F的速度为 $\sqrt{3}$个单位每秒，运动时间为x秒，△AEF的面积为y，求y关于x的函数解析式，并指出当x为何值时，y的值最大，最大值为多少？

（3）如图3，H在线段AB上且 $AH=\frac{1}{3}HB$，M为DF的中点，当点E、F分别在线段AD、AB上运动时，探究点E、F在什么位置能使 $EM＝HM$，并说明理由．

在平面直角坐标系 $\mathit{xOy}$ 中，⊙ O 的半径为 1 ， A ， B 为⊙ O 外两点， $AB=1$ ．给出如下定义：平移线段 AB ，得到⊙ O 的弦 $A^{\text{'}}{B}^{\text{'}}$ （ $A^{\text{'}},B^{\text{'}}$ 分别为点 A ， B 的对应点），线段 $A{A}^{\text{'}}$ 长度的最小值称为线段 AB 到⊙ O 的"平移距离"．

（ 1 ）如图，平移线段 AB 到⊙ O 的长度为 1 的弦 $P_1{P}_2$ 和 $P_3{P}_4$ ，则这两条弦的位置关系是            ；在点 $P_1,P_2,P_3,P_4$ 中，连接点 A 与点         的线段的长度等于线段 AB 到⊙ O 的"平移距离"；

（ 2 ）若点 A ， B 都在直线 $y=\sqrt{3}x+2\sqrt{3}$ 上，记线段 AB 到⊙ O 的"平移距离"为 $d_1$ ，求 $d_1$ 的最小值；

（ 3 ）若点 A 的坐标为 $\left(2,\frac{3}{2}\right)$ ，记线段 AB 到⊙ O 的"平移距离"为 $d_2$ ，直接写出 $d_2$ 的取值范围．

如图，在直角坐标系中，二次函数经过 $A\left(-2,0\right)$ ， $B\left(2,2\right)$ ， $C\left(0,2\right)$ 三个点．

（ 1 ）求该二次函数的解析式．

（ 2 ）若在该函数图象的对称轴上有个动点 $D$ ，求当 $D$ 点坐标为何值时， $△\mathit{ACD}$ 的周长最小．

如图，在平面直角坐标系中，抛物线 $y=a{x}^2+\mathit{bx}-2$ 交 $x$ 轴于 $A$ ， $B$ 两点，交 $y$ 轴于点 $C$ ，且 $\mathit{OA}=2\mathit{OC}=8\mathit{OB}$ ，点 $P$ 是第三象限内抛物线上的一动点．

（ 1 ）求此抛物线的表达式；

（ 2 ）若 $\mathit{PC}//\mathit{AB}$ ，求点 $P$ 的坐标；

（ 3 ）连接 $\mathit{AC}$ ，求 $\Delta PAC$ 面积的最大值及此时点 $P$ 的坐标．

如图 ① ，直线 $l$ 经过点 $（4，0）$ 且平行于 y 轴，二次函数 $y＝a{x}^2﹣2ax+c（a、c\mathrm{是常数}，a＜0）$ 的图象经过点 $M(﹣1，1)$ ，交直线 $l$ 于点 N ，图象的顶点为 D ，它的对称轴与 x 轴交于点 C ，直线 DM 、 DN 分别与 x 轴相交于 A 、 B 两点．

（ 1 ）当 $a＝﹣1$ 时，求点 N 的坐标及 $\frac{\mathit{AC}}{\mathit{BC}}$ 的值；

（ 2 ）随着 a 的变化， $\frac{\mathit{AC}}{\mathit{BC}}$ 的值是否发生变化？请说明理由；

（ 3 ）如图 ② ， E 是 x 轴上位于点 B 右侧的点， $BC＝2BE$ ， DE 交抛物线于点 F ．若 $FB＝FE$ ，求此时的二次函数表达式．

如图，在平面直角坐标系中，矩形 $\mathit{ABCD}$ 的边 $\mathit{AB}$ 长是方程 $x^2-3x-18=0$ 的根，连接 $\mathit{BD}$ ， $\angle \mathit{DBC}=30°$ ，并过点 $C$ 作 $\mathit{CN}\perp \mathit{BD}$ ，垂足为 $N$ ，动点 $P$ 从点 $B$ 以每秒 $2$ 个单位长度的速度沿 $\mathit{BD}$ 方向匀速运动到点 $D$ 为止；点 $M$ 沿线段 $\mathit{DA}$ 以每秒 $\sqrt{3}$ 个单位长度的速度由点 $D$ 向点 $A$ 匀速运动，到点 $A$ 为止，点 $P$ 与点 $M$ 同时出发，设运动时间为 $t$ 秒 $\left(t>0\right)$

（ 1 ）线段 $\mathit{CN}=$ ______ ；

（ 2 ）连接 $\mathit{PM}$ 和 $\mathit{MN}$ ，求 $\Delta PMN$ 的面积 $s$ 与运动时间 $t$ 的函数关系式；

（ 3 ）在整个运动过程中，当 $\Delta PMN$ 是以 $\mathit{PN}$ 为腰的等腰三角形时，直接写出点 $P$ 的坐标．

发现规律：

（ 1 ）如图①， $△\mathit{ABC}$ 与 $△\mathit{ADE}$ 都是等边三角形，直线 $\mathit{BD},\mathit{CE}$ 交于点 $F$ ．直线 $\mathit{BD}$ ， $\mathit{AC}$ 交于点 $H$ ．求 $\angle \mathit{BFC}$ 的度数

（ 2 ）已知： $△\mathit{ABC}$ 与 $△\mathit{ADE}$ 的位置如图②所示，直线 $\mathit{BD},\mathit{CE}$ 交于点 $F$ ．直线 $\mathit{BD}$ ， $\mathit{AC}$ 交于点 $H$ ．若 $\angle \mathit{ABC}=\angle \mathit{ADE}=\alpha$ ， $\angle \mathit{ACB}=\angle \mathit{AED}=\beta$ ，求 $\angle \mathit{BFC}$ 的度数

应用结论：

（ 3 ）如图③，在平面直角坐标系中，点 $O$ 的坐标为 $(0,0)$ ，点 $M$ 的坐标为 $(3,0)$ ， $N$ 为 $y$ 轴上一动点，连接 $\mathit{MN}$ ．将线段 $\mathit{MN}$ 绕点 $M$ 逆时针旋转 ${60}^{\circ }$ 得到线段 $\mathit{MK}$ ，连接 $\mathit{NK}$ ， $\mathit{OK}$ ，求线段 $\mathit{OK}$ 长度的最小值

如图，在平面直角坐标系中，抛物线 $y=a{x}^2+\mathit{bx}-4(a\ne 0)$ 与 $x$ 轴交于点 $A(-1,0)$ ， $B(4,0)$ ，与 $y$ 轴交于点 $C$ ．

（1）求该抛物线的解析式；

（2）直线 $l$ 为该抛物线的对称轴，点 $D$ 与点 $C$ 关于直线 $l$ 对称，点 $P$ 为直线 $\mathit{AD}$ 下方抛物线上一动点，连接 $\mathit{PA}$ ， $\mathit{PD}$ ，求 $\mathit{\Delta PAD}$ 面积的最大值．

（3）在（2）的条件下，将抛物线 $y=a{x}^2+\mathit{bx}-4(a\ne 0)$ 沿射线 $\mathit{AD}$ 平移 $4\sqrt{2}$ 个单位，得到新的抛物线 $y_1$ ，点 $E$ 为点 $P$ 的对应点，点 $F$ 为 $y_1$ 的对称轴上任意一点，在 $y_1$ 上确定一点 $G$ ，使得以点 $D$ ， $E$ ， $F$ ， $G$ 为顶点的四边形是平行四边形，写出所有符合条件的点 $G$ 的坐标，并任选其中一个点的坐标，写出求解过程．

盲盒为消费市场注入了活力，既能够营造消费者购物过程中的趣味体验，也为商家实现销售额提升拓展了途径．某商家将蓝牙耳机、多接口优盘、迷你音箱共22个，搭配为 $A$， $B$， $C$三种盲盒各一个，其中 $A$盒中有2个蓝牙耳机，3个多接口优盘，1个迷你音箱； $B$盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量，蓝牙耳机与迷你音箱的数量之比为 $3:2$； $C$盒中有1个蓝牙耳机，3个多接口优盘，2个迷你音箱．经核算， $A$盒的成本为145元， $B$盒的成本为245元（每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和），则 $C$盒的成本为　　元．

如图，在平面直角坐标系中，矩形 $\mathit{ABCD}$ 的顶点 $A$ ， $B$ 在 $x$ 轴的正半轴上，反比例函数 $y=\frac{k}{x}(k>0,x>0)$ 的图象经过顶点 $D$ ，分别与对角线 $\mathit{AC}$ ，边 $\mathit{BC}$ 交于点 $E$ ， $F$ ，连接 $\mathit{EF}$ ， $\mathit{AF}$ ．若点 $E$ 为 $\mathit{AC}$ 的中点， $\mathit{\Delta AEF}$ 的面积为1，则 $k$ 的值为 $($ 　　 $)$

A．

$\frac{12}{5}$

B．

$\frac{3}{2}$

C．

2

D．

3

关于 $x$ 的分式方程 $\frac{\mathit{ax}-3}{x-2}+1=\frac{3x-1}{2-x}$ 的解为正数，且使关于 $y$ 的一元一次不等式组 $\left\{\begin{array}{c}\frac{3y-2}{2}⩽y-1\\ y+2>a\end{array}\right.$ 有解，则所有满足条件的整数 $a$ 的值之和是 $($ 　　 $)$

A．

$-5$

B．

$-4$

C．

$-3$

D．

$-2$