在平面直角坐标系 中,⊙ O 的半径为 1 , A , B 为⊙ O 外两点, .给出如下定义:平移线段 AB ,得到⊙ O 的弦 ( 分别为点 A , B 的对应点),线段 长度的最小值称为线段 AB 到⊙ O 的"平移距离".

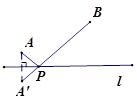
( 1 )如图,平移线段 AB 到⊙ O 的长度为 1 的弦 和 ,则这两条弦的位置关系是 ;在点 中,连接点 A 与点 的线段的长度等于线段 AB 到⊙ O 的"平移距离";
( 2 )若点 A , B 都在直线 上,记线段 AB 到⊙ O 的"平移距离"为 ,求 的最小值;
( 3 )若点 A 的坐标为 ,记线段 AB 到⊙ O 的"平移距离"为 ,直接写出 的取值范围.
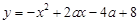
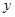 随
随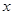 的增大而减小,求
的增大而减小,求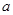 的取
的取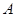 为一个顶点作该二次函数图象的内接正三角形
为一个顶点作该二次函数图象的内接正三角形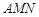 (M,N两点在二次函数的图象上),请问:△
(M,N两点在二次函数的图象上),请问:△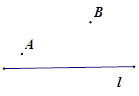



 的值.
的值. 的图象与反比例函数
的图象与反比例函数
 的图象交于
的图象交于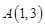 ,
,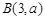 两点.
两点.
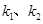 的值;
的值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号