如图,在平面直角坐标系中,抛物线 与 轴交于点 , ,与 轴交于点 .
(1)求该抛物线的解析式;
(2)直线 为该抛物线的对称轴,点 与点 关于直线 对称,点 为直线 下方抛物线上一动点,连接 , ,求 面积的最大值.
(3)在(2)的条件下,将抛物线 沿射线 平移 个单位,得到新的抛物线 ,点 为点 的对应点,点 为 的对称轴上任意一点,在 上确定一点 ,使得以点 , , , 为顶点的四边形是平行四边形,写出所有符合条件的点 的坐标,并任选其中一个点的坐标,写出求解过程.

相关知识点
推荐套卷
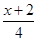 ≤
≤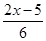 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来 :
: 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,抛物线
,抛物线 过点
过点 ,其中
,其中 >0,又点
>0,又点 是抛物线的对称轴
是抛物线的对称轴 上一动点.
上一动点. 上找一点
上找一点 ,使
,使 周长的最小值为
周长的最小值为 ,求抛物线的解析式及顶点
,求抛物线的解析式及顶点 的坐标;
的坐标; 上有一动点
上有一动点 以每秒2个单位的速度从点
以每秒2个单位的速度从点 移动(
移动( ∥
∥ 交
交 ,设
,设 秒,试把△
秒,试把△ 的面积
的面积 表示成时间
表示成时间
 (0°<
(0°<
 的图象与边BC交于点F.
的图象与边BC交于点F.
 .且
.且 ,求k的值.
,求k的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号