如图1,隧道截面由抛物线的一部分AED和矩形ABCD构成,矩形的一边BC为12米,另一边AB为2米.以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系 ,规定一个单位长度代表1米.E 是抛物线的顶点.
(1)求此抛物线对应的函数表达式;
(2)在隧道截面内(含边界)修建“ ”型或“
”型或“ ”型栅栏,如图2、图3中粗线段所示,点
在x轴上,MN与矩形
的一边平行且相等.栅栏总长l为图中粗线段
MN长度之和,请解决以下问题:
”型栅栏,如图2、图3中粗线段所示,点
在x轴上,MN与矩形
的一边平行且相等.栅栏总长l为图中粗线段
MN长度之和,请解决以下问题:
(ⅰ)修建一个“ ”型栅栏,如图2,点
在抛物线AED上.设点P1的横坐标为
,求栅栏总长l与m之间的函数表达式和l的最大值;
”型栅栏,如图2,点
在抛物线AED上.设点P1的横坐标为
,求栅栏总长l与m之间的函数表达式和l的最大值;
(ⅱ)现修建一个总长为18的栅栏,有如图3所示的“ ”型和“
”型和“ ”型两种设计方案,请你从中选择一种,求出该方案下矩形
面积的最大值,及取最大值时点P1的横坐标的取值范围(P1在P4右侧).
”型两种设计方案,请你从中选择一种,求出该方案下矩形
面积的最大值,及取最大值时点P1的横坐标的取值范围(P1在P4右侧).



 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.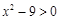 .
. ,
, .
. (2)
(2)
 ,
,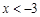 ,
,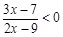 的解集;
的解集;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号