高中物理探究向心力大小与半径、角速度、质量的关系计算题

如图所示，水平的粗糙轨道与竖直的光滑圆形轨道相连，圆形轨道间不相互重叠，即小球离开圆形轨道后可继续沿水平轨道运动。圆形轨道半径R=0.2m，右侧水平轨道BC长为L=4m，C点右侧有一壕沟，C、D两点的竖直高度h=lm，水平距离s=2m，小球与水平轨道间的动摩擦因数μ=0．2，重力加速度g=l0m/s²。一小球从圆形轨道最低点B以某一水平向右的初速度出发，进入圆形轨道。

（1）若小球通过圆形轨道最高点A时给轨道的压力大小恰为小球的重力大小，求小球在B点的初速度多大？
（2）若小球从B点向右出发，在以后的运动过程中，小球既不脱离圆形轨道，又不掉进壕沟，求小球在B点的初速度的范围是多大？

如图所示，一质点沿半径R=20m的圆周自A点出发，顺时针方向运动了10s第一次到达B点．求：

（1）这一过程中质点的路程；
（2）这一过程中质点位移的大小和方向；
（3）这一过程中质点平均速度的大小．

如图，质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a，从距BC高h的A处由静止释放，沿ABC光滑轨道滑下，在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度，悬挂b球的细绳能承受的最大拉力为2.8mg。试问：

①a与b球碰前瞬间的速度多大？
②a、b两球碰后，细绳是否会断裂？(要求通过计算回答)

如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接．在过圆心O的水平界面MN的下方分布有水平向右的匀强电场．现有一个质量为m、电荷量为q的带正电小球在水平轨道上的A点由静止释放，小球运动到C点离开半圆轨道后，经界面MN上的P点进入电场(P点恰好在A点的正上方，小球可视为质点，小球运动到C点之前所带电荷量保持不变，经过C点后所带电荷量立即变为零)．已知A、B两点间的距离为2R，重力加速度为g.在上述运动过程中，求：
 
（1）电场强度E的大小；
（2）小球在半圆轨道上运动时的最大速率．

石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖。用石墨烯制作超级缆绳,人类搭建“太空电梯”的梦想有望在本世纪实现。科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换。（地面附近重力加速度g取10 m/s²,地球自转角速度ω=7.2×10^-5rad/s,地球半径R=6.4×10³km。计算结果保留3位有效数字）

(1)若“太空电梯”将货物从赤道基站运到距地面高度为h₁=17R/3的同步轨道站,求轨道站内的人相对地心运动的速度大小。
(2)当电梯仓停在距地面高度h₂=2R的站点时,求仓内质量m₂="54" kg的人对水平地板的压力大小。

如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度转动，盘面上离转轴距离r=0.1m处有一质量为0.1kg的小物体恰好能与圆盘始终保持相对静止．物体与盘面间的动摩擦因数为0.8（设最大静摩擦力等于滑动摩擦力），盘面与水平面的夹角为37°（g=10m/s²，sin37°=0.6），求：

（1）圆盘转动的角速度ω的大小；
（2）小物体运动到最高点时受到的摩擦力.

如图所示，四分之三周长的细圆管的半径R=0.4m，管口B和圆心O在同一水平面上，D是圆管的最高点，其中半圆周BE段存在摩擦，BC和CE段动摩擦因数相同，ED段光滑；质量m=0.5kg、直径稍小于圆管内径的小球从距B正上方高H=2.5m的A处自由下落，从B处进入圆管继续运动直到圆管的最高点D飞出，恰能再次飞到B处．重力加速度g=10m/s²．求：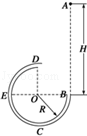

（1）小球飞离D点时的速度；
（2）小球在D点时对轨道的压力大小和方向；
（3）小球从B点到D点过程中克服摩擦所做的功．

如图所示，竖直平面内的半圆形轨道下端与水平面相切，B、C分别为半圆形轨道的最低点和最高点。小滑块（可视为质点）沿水平面向左滑动，经过A点时的速度v_A=6.0m/s。已知半圆形轨道光滑，半径R=0.40m，滑块与水平面间的动摩擦因数m =0.50，A、B两点间的距离l=1.10m。取重力加速度g=10m/s²。求：

（1）滑块运动到B点时速度的大小v_B；
（2）滑块运动到C点时速度的大小v_C；
（3）滑块从C点水平飞出后，落地点与B点间的距离x。

如图所示，两根等高的四分之一光滑圆弧轨道，半径为r、间距为L，图中oa水平，co竖直，在轨道顶端连有一阻值为R的电阻，整个装置处在一竖直向上的匀强磁场中，磁感应强度为B。现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑，到达轨道底端cd时受到轨道的支持力为2mg。整个过程中金属棒与导轨接触良好，轨道电阻不计，求：

(1)金属棒到达轨道底端cd时的速度大小和通过电阻R的电流：
(2)金属棒从ab下滑到cd过程中回路中产生的焦耳热和通过R的电荷量：
(3)若金属棒在拉力作用下，从cd开始以速度v₀向右沿轨道做匀速圆周运动，则在到达ab的过程中拉力做的功为多少?

如图甲所示，BCD为竖直放置的半径R=0.20m的半圆形轨道，在半圆形轨道的最低位置B和最高位置D均安装了压力传感器，可测定小物块通过这两处时对轨道的压力F_B和F_D。半圆形轨道在B位置与水平直轨道AB平滑连接，在D位置与另一水平直轨道EF相对，其间留有可让小物块通过的缝隙。一质量m=0.20kg的小物块P（可视为质点），以不同的初速度从M点沿水平直轨道AB滑行一段距离，进入半圆形轨道BCD经过D位置后平滑进入水平直轨道EF。一质量为2m的小物块Q（可视为质点）被锁定在水平直轨道EF上，其右侧固定一个劲度系数为k=500N/m的轻弹簧。如果对小物块Q施加的水平力F≥30N，则它会瞬间解除锁定沿水平直轨道EF滑行，且在解除锁定的过程中无能量损失。已知弹簧的弹性势能公式,其中k为弹簧的劲度系数，x为弹簧的形变量。g取10m/s²。

（1）通过传感器测得的F_B和F_D的关系图线如图乙所示。若轨道各处均不光滑，且已知轨道与小物块P之间的动摩擦因数μ=0.10，MB之间的距离x_MB=0.50m。当 F_B=18N时，求：
①小物块P通过B位置时的速度v_B的大小；
②小物块P从M点运动到轨道最高位置D的过程中损失的总机械能；
（2）若轨道各处均光滑，在某次实验中，测得P经过B位置时的速度大小为m/s。求在弹簧被压缩的过程中，弹簧的最大弹性势能。

如图所示，粗糙水平面与半径R=1.5m的光滑圆弧轨道相切于B点，质量m=1kg的物体在大小为10N、方向与水平面成37°角的拉力F作用下从A点由静止开始沿水平面运动，到达B点时立刻撤去F，物体沿光滑圆弧向上冲并越过C点，然后返回经过B处的速度v_B=15m/s。已知s_AB=15m，g=10m/s²，sin37°=0.6，cos37°=0.8。求：

（1）物体到达C点时对轨道的压力和物体越过C点后上升的最大高度h；
（2）物体与水平面的动摩擦因数μ。

如图所示，质量为m的b球用长为h的细绳悬挂于水平轨道BC的出口C处。质量也为m的a球，从距BC高为h的A处由静止释放，沿光滑轨道ABC滑下，在C处与b球正碰并与b球粘在一起。已知BC轨道距地面有一定的高度，悬挂b球的细绳能承受的最大拉力为2.8mg。求：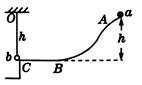

（1）ab碰后的速度多大；
（2）a与b碰后细绳是否会断裂。

如图所示，光滑的圆弧轨道与倾角为θ=37°的斜面相切于B点，圆弧轨道的半径为R=1m，质量为M=2kg的物块甲在斜面上A点由静止释放，物块甲与斜面的动摩擦因数为μ=0.25，AB间距离为s=4m，当甲运动到C点时，恰好与迎面过来的质量m=0.5kg的乙相碰，碰后两者粘在一起，向左运动，恰好能到达圆弧轨道的最高点D点，（已知sin37°=0.6，cos37°=0.8，g取10m/s²）求：

（1）物块甲与物块乙相碰前的速度v₁；
（2）物块甲和乙碰撞后的一瞬间，它们对圆弧轨道最低点C的压力之和；
（3）两物块从D点抛出后，落到斜面上所用的时间．

如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴重合，转台以一定角速度匀速旋转，一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与之间的夹角为60°。已知重力加速度大小为，小物块与陶罐之间的最大静摩擦力大小为。

（1）若小物块受到的摩擦力恰好为零，求此时的角速度；
（2）若小物块一直相对陶罐静止，求陶罐旋转的角速度的取值范围。

如图所示，在竖直平面的xoy坐标系内，一根长为l的不可伸长的细绳，一端固定在拉力传感器A上，另一端系一质量为m的小球．x轴上的P点固定一个表面光滑的小钉，P点与传感器A相距．现拉小球使细绳绷直并处在水平位置，然后由静止释放小球，当细绳碰到钉子后，小球可以绕钉子在竖直平面内做圆周运动．已知重力加速度大小为g，求：

（1）若小球经过最低点时拉力传感器的示数为7mg，求此时小球的速度大小；
（2）传感器A与坐标原点O之间的距离；
（3）若小球经过最低点时绳子恰好断开，请确定小球经过y轴的位置．