如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度转动，盘面上离转轴距离r=0.1m处有一质量为0.1kg的小物体恰好能与圆盘始终保持相对静止．物体与盘面间的动摩擦因数为0.8（设最大静摩擦力等于滑动摩擦力），盘面与水平面的夹角为37°（g=10m/s2，sin37°=0.6），求：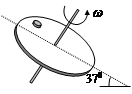
（1）圆盘转动的角速度ω的大小；
（2）小物体运动到最高点时受到的摩擦力.
(14分)如图18(a)所示，质量m＝1 kg的物体沿倾角θ＝37°的固定粗糙斜面由静止开始
向下运动，风对物体的作用力沿水平方向向右，其大小与风速v成正比，比例系数用k
表示，物体加速度a与风速v的关系如图(b)所示，求：(sin37°＝0.6，cos37°＝0.8，g＝
10 m/s2)
(1)物体与斜面间的动摩擦因数μ；
(2)比例系数k.
(12分)为了测量某住宅大楼每层的平均高度(层高)及电梯运行情况，甲、乙两位同学在一楼电梯内用电子体重计及秒表进行了以下实验．质量为m＝50 kg的甲同学站在体重计上，乙同学记录电梯从地面一楼到顶层全过程中，体重计示数随时间变化的情况，并作出了如图17所示的图象，已知t＝0时，电梯静止不动，从电梯内楼层按钮上获知该大楼共19层．g取10 m/s2，求：
(1)电梯启动和制动的加速度大小．
(2)电梯上升的总高度及该大楼的层高．
(10分)如图16所示，斜面体质量为M，倾角为θ，与水平面间的动摩擦因数为μ，用细绳竖直悬挂一质量为m的小球静止在光滑斜面上，当烧断绳的瞬间，至少以多大的水平向右的力由静止拉动斜面体，小球才能做自由落体运动到地面？
(14分)消防队员为缩短下楼的时间，往往抱着竖直的杆直接滑下．假设一名质量为60 kg、
训练有素的消防队员从七楼(即离地面18 m的高度)抱着竖直的杆以最短的时间滑下．已
知杆的质量为200 kg，消防队员着地的速度不能
大于6 m/s，手和腿对杆的最大压力为1800 N，手和腿与杆之间的动摩擦因数为0.5，设
当地的重力加速度 g＝10 m/s2.假设杆是固定在地面上的，杆在水平方向不移动．试求：
(1)消防队员下滑过程中的最大速度；
(2)消防队员下滑过程中杆对地面的最大压力；
(3)消防队员下滑的最短的时间．
粤公网安备 44130202000953号