高中物理探究向心力大小与半径、角速度、质量的关系计算题

如图所示，是一种测定风力的仪器，P是质量为200g的金属球，固定在一根细长钢性的金属丝下端，当无风时金属球自然竖直下垂，有风时金属丝将偏离竖直方向，刻度盘上的角度就能反映出风力的大小。若某一时刻风从图示的水平方向吹向金属球P时，金属丝向左偏离竖直方向的角度θ=30°而处于静止状态。取g=10m/s²    则：

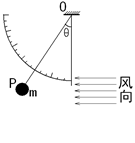
（1）此时风力和金属丝拉力分别有多大？
（2）有人说：“若角度变为2θ，则风力也变为原来的2倍”，你认为这个结论对不对？为什么？

在一级方程式汽车大赛中，一辆赛车的总质量为m，一个路段的水平转弯半径为R，赛车转此弯时的速度为v，赛车形状都设计得使其上下方空气有一压力差﹣﹣气动压力，从而增大了对地面的正压力．正压力与摩擦力的比值叫侧向附着系数，以η表示．要上述赛车转弯时不侧滑，则需要多大的气压动力？

“翻滚过上车”的物理原理可以用如图所示装置演示。光滑斜槽轨道AD与半径为的竖直圆轨道（圆心为O）相连，AD与圆O相切于D点，B为轨道的最低点，。质量的小球从距D点处由静止开始下滑，然后冲上光滑的圆形轨道（取，，）。求：

（1）小球进入圆轨道D点时对轨道压力的大小；
（2）小球通过B点时加速度；
（3）试分析小球能否通过竖直圆轨道的最高点C，并说明理由。

一质量为2000 kg的汽车，行驶到一座半径为40m的圆弧形拱桥顶端时，汽车运动速度为8m/s。求此时汽车对桥面的压力的大小（g=10m/s²）。

如图所示，在第Ⅱ象限内有水平向右的匀强电场，电场强度为E，在第Ⅰ、Ⅳ象限内分别存在如图所示的匀强磁场，磁感应强度大小相等，有一个带电粒子以垂直于x轴的初速度v₀从x轴上的P点进入匀强电场中，并且恰好与y轴的正方向成45°角进入磁场，又恰好垂直x轴进入第Ⅳ象限的磁场，已知OP之间的距离为d，（不计粒子重力）求：

（1）带电粒子在磁场中做圆周运动的半径；
（2）带电粒子从进入磁场到第二次经过x轴，在磁场中运动的总时间；
（3）匀强磁场的磁感应强度大小。

一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△ω与对应时间△t的比值定义为角加速度β。我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D…为计数点，相邻两计数点间有四个点未画出）

①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，圆盘停止转动和打点，取下纸带，进行测量。
（1）用20分度的游标卡尺测得圆盘的直径如图乙所示，圆盘的直径d为______cm；
（2）由图丙可知，打下计数点D时，圆盘转动的角速度为______rad/s  （计算结果保留3位有效数字）
（3）圆盘转动的角加速度大小为______rad/s²。（计算结果保留3位有效数字）

如图所示，是马戏团中上演的飞车节目，在竖直平面内有半径为R的圆轨道．表演者骑着摩托车在圆轨道内做圆周运动．已知人和摩托车的总质量为m，人以v₁＝的速度过轨道最高点B，并以v₂＝v₁的速度过最低点A.求在A、B两点轨道对摩托车的压力大小相差多少？

一辆质量m=2.0×10³kg的汽车，经过半径r=50m的水平弯路．则：
（1）当汽车的速度v=10m/s时，受到的向心力为多大？
（2）若汽车轮胎与路面间的最大静摩擦力F_m=9.0×10³N，为了使这辆车通过此段弯路时不发生侧滑，行驶的最大速度为多大？

轻杆长L=1.5m，以一端为圆心，在竖直面内做圆周运动，杆另一端固定一个质量m=1.8kg小球，小球通过最高点时速率v=3m/s，求此时小球对杆的作用力大小及方向（g=10m/s²）。

如图所示，半径为R，内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时，对管壁上部的压力为3mg，b通过最高点A时，对管壁下部的压力为0.75 mg，求a、b两球落地点间的距离。

如图所示，M是水平放置的半径足够大的圆盘，绕过其圆心的竖直轴匀速转动，以经过O水平向右的方向作为x轴的正方向 在圆心O正上方距盘面高为h处有一个正在间断滴水的容器，在t＝0时刻开始随传送带沿与x轴平行的方向做匀速直线运动，速度大小为v 已知容器在t＝0时滴下第一滴水，以后每当前一滴水刚好落到盘面上时再滴一滴水 问：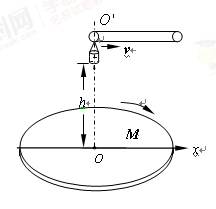

（1）每一滴水经多长时间滴落到盘面上？
（2）要使每一滴水在盘面上的落点都位于一条直线上，圆盘转动的最小角速度ω
（3）第二滴水与第三滴水在盘面上的落点间的最大距离s

如图所示，在竖直平面内，由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道，AB与BC的连接处是半径很小的圆弧，BC与CD相切，圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求：

（1）小物块通过B点时速度v_B的大小；
（2）试通过计算说明，小物块能否通过圆形轨道的最高点D。

在如图所示的圆锥摆中，已知绳子长度为L ，绳子转动过程中与竖直方向的夹角为θ ，试求小球做圆周运动的周期。

长为L的细线，拴一质量为m的小球，一端固定于O点。让其在水平面内做匀速圆周运动（这种运动通常称为圆锥摆运动），如图所示。当摆线L与竖直方向的夹角是时，求：

（1）线的拉力F；
（2）小球运动的线速度大小；

一同学骑自行车在水平公路上以5 m/s的恒定速率转弯，已知人和车的总质量m＝80 kg，转弯的路径近似看成一段圆弧，圆弧半径R＝20m，求：
(1)人和车作为一个整体转弯时需要的向心力；
(2)若车胎和路面间的动摩擦因数μ＝0.5，为安全转弯，车速不能超过多少？(设最大静摩擦力等于滑动摩擦力，g取10 m/s²)