如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求: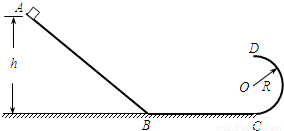
(1)小物块通过B点时速度vB的大小;
(2)试通过计算说明,小物块能否通过圆形轨道的最高点D。
相关知识点
如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求:
(1)小物块通过B点时速度vB的大小;
(2)试通过计算说明,小物块能否通过圆形轨道的最高点D。