如图所示,水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m.在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度E=1.0×104N/C.现有一电荷量q=+1.0×10﹣4C,质量m=0.10kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取g=10m/s2.试求:
(1)带电体在圆形轨道C点的速度大小.
(2)D点到B点的距离xDB.
(3)带电体运动到圆形轨道B点时对圆形轨道的压力大小.
(4)带电体在从P开始运动到落至D点的过程中的最大动能.
如图所示,四分之三周长的细圆管的半径R=0.4m,管口B和圆心O在同一水平面上,D是圆管的最高点,其中半圆周BE段存在摩擦,BC和CE段动摩擦因数相同,ED段光滑;质量m=0.5kg、直径稍小于圆管内径的小球从距B正上方高H=2.5m的A处自由下落,从B处进入圆管继续运动直到圆管的最高点D飞出,恰能再次飞到B处.重力加速度g=10m/s2.求: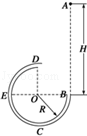
(1)小球飞离D点时的速度;
(2)小球在D点时对轨道的压力大小和方向;
(3)小球从B点到D点过程中克服摩擦所做的功.
粗糙水平轨道AB与竖直平面内的光滑圆弧轨道BC相切于B点,一物块(可看成为质点)在水平向右的恒力F作用下自水平轨道的P点处由静止开始匀加速运动到B,此时撤去该力,物块滑上圆弧轨道,在圆弧轨道上运动一段时间后,回到水平轨道,恰好返回到P点停止运动,已知物块在圆弧轨道上运动时对轨道的压力最大值为F1=2.02N,最小值为F2=1.99N,当地重力加速度为g=10m/s2.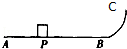
(1)求物块的质量m的大小;
(2)若已知圆弧轨道的半径为R=8m,P点到B点的距离是x=0.5m,求F的大小.
如图所示,在光滑绝缘的水平面上,放置两块直径为2L的同心半圆形金属板A、B,两板间的距离很近,半圆形金属板A、B的左边有水平向右的匀强电场E1,半圆形金属板A、B之间存在电场,两板间的电场强度E2可认为大小处处相等,方向都指向O,现从正对A、B板间隙、到两板的一端距离为d处静止释放一个质量为m、电荷量为q的带正电微粒(不计重力),此微粒恰能在两板间运动且不与板发生相互作用.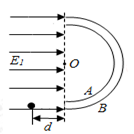
(1)求半圆形金属板A、B之间电场强度的E2的大小?
(2)从释放微粒开始,经过多长时间微粒的水平位移最大?
质量为1kg的小球用长为0.5m的细线悬挂在O点,O点距地面高度为1m,如果使小球绕OO′轴在水平面内做圆周运动,若细线受到拉力为12.5N就会被拉断。求: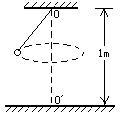
(1)当小球的角速度为多大时线将断裂?
(2)小球落地点与悬点的水平距离。(g取10 m/s2)
如图所示,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左。静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向沿圆弧半径指向圆心O。离子质量为m、电荷量为q, 、
、 ,离子重力不计。
,离子重力不计。
(1)求圆弧虚线对应的半径R的大小;
(2)若离子恰好能打在QN板的中点上,求矩形区域QNCD内匀强电场场强E的值;
(3)若撤去矩形区域QNCD内的匀强电场,换为垂直纸面向里的匀强磁场,且离子恰能从QN板下端飞出QNCD区域,求磁场磁感应强度B。
如图所示,水平轨道MN与竖直光滑半圆轨道相切于N点,轻弹簧左端固定在轨道的M点,将一质量为m=1kg的小物块靠在弹簧右端并压缩至O点,此时弹簧储有弹性势能Ep,现将小物块无初速释放,小物块恰能通过轨道最高点B,此后水平飞出再落回到水平面。已知ON的距离L=3.0m,小物块与水平轨道间的动摩擦因数μ=0.2,圆轨道半径R=0.4m,g取10 m/s2。求: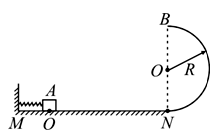
(1)小物块通过B点抛出后,落地点距N的水平距离x;
(2)弹簧储有的弹性势能Ep。
如图所示,长度为l的细绳上端固定在天花板上O点,下端栓这质量为m的小球。当把细绳拉直时,细绳与竖直线夹角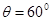 ,此时小球静止与光滑的水平面上。
,此时小球静止与光滑的水平面上。
(1)当球以角速度 做圆锥摆运动时,细绳的张力
做圆锥摆运动时,细绳的张力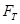 为多大?水平面受到的压力N是多大?
为多大?水平面受到的压力N是多大?
(2)当球以角速度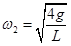 做圆锥摆运动时,细绳的张力
做圆锥摆运动时,细绳的张力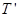 为多大?水平面受到的压力
为多大?水平面受到的压力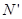 是多大?
是多大?
“翻滚过上车”的物理原理可以用如图所示装置演示。光滑斜槽轨道AD与半径为 的竖直圆轨道(圆心为O)相连,AD与圆O相切于D点,B为轨道的最低点,
的竖直圆轨道(圆心为O)相连,AD与圆O相切于D点,B为轨道的最低点, 。质量
。质量 的小球从距D点
的小球从距D点 处由静止开始下滑,然后冲上光滑的圆形轨道(取
处由静止开始下滑,然后冲上光滑的圆形轨道(取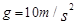 ,
, ,
, )。求:
)。求:
(1)小球进入圆轨道D点时对轨道压力的大小;
(2)小球通过B点时加速度;
(3)试分析小球能否通过竖直圆轨道的最高点C,并说明理由。
如图所示,AB是位于竖直平面内、半径R=0.5 m的 圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103 N/C.今有一质量为m=0.1 kg、带电荷量q=+8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10 m/s2,求:
圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103 N/C.今有一质量为m=0.1 kg、带电荷量q=+8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10 m/s2,求:
(1) 小滑块第一次经过圆弧形轨道最低点B时对B点的压力;
(2) 小滑块运动到右侧最远处到最低点B的距离;
(3) 小滑块在水平轨道上通过的总路程。
如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回.已知R=0.4m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计.取g=10m/s2.求: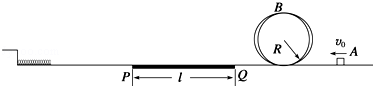
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
如图所示,在第Ⅱ象限内有水平向右的匀强电场,电场强度为E,在第Ⅰ、Ⅳ象限内分别存在如图所示的匀强磁场,磁感应强度大小相等,有一个带电粒子以垂直于x轴的初速度v0从x轴上的P点进入匀强电场中,并且恰好与y轴的正方向成45°角进入磁场,又恰好垂直x轴进入第Ⅳ象限的磁场,已知OP之间的距离为d,(不计粒子重力)求:
(1)带电粒子在磁场中做圆周运动的半径;
(2)带电粒子从进入磁场到第二次经过x轴,在磁场中运动的总时间;
(3)匀强磁场的磁感应强度大小。
如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求:
(1)小物块通过B点时速度vB的大小;
(2)试通过计算说明,小物块能否通过圆形轨道的最高点D。
一个质量为m电荷量为q的带电粒子从x轴上的P(a,0)点以速度v,沿与x正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限,不计重力.求:
(1)粒子做圆周运动的半径R
(2)匀强磁场的磁感应强度B.