已知椭圆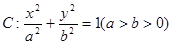 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为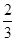 ,短轴长为
,短轴长为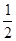 ,直线
,直线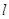 与椭圆C交于M、N两点。
与椭圆C交于M、N两点。
(1)求椭圆C的方程;
(2)若直线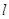 与圆
与圆 相切,证明:
相切,证明: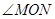 为定值
为定值
已知直线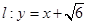 ,圆
,圆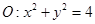 ,椭圆
,椭圆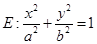
 的离心率
的离心率 ,直线
,直线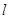 被圆
被圆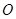 截得的弦长与椭圆的短轴长相等.
截得的弦长与椭圆的短轴长相等.

 求椭圆
求椭圆 的方程;
的方程;
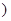 已知动直线
已知动直线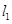 (斜率存在)与椭圆
(斜率存在)与椭圆 交于
交于 两个不同点,且△
两个不同点,且△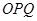 的面积为
的面积为 ,若
,若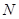 为线段
为线段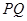 的中点,问:在
的中点,问:在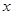 轴上是否存在两个定点
轴上是否存在两个定点 使得直线
使得直线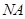 与
与 的斜率之积为定值?若存在,求出
的斜率之积为定值?若存在,求出 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知椭圆
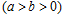 上的一动点
上的一动点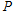 到右焦点的最短距离为
到右焦点的最短距离为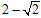 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.
(1)求椭圆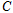 的方程;
的方程;
(2)设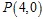 ,
,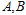 是椭圆
是椭圆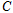 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结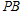 交椭圆
交椭圆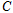 于另一点
于另一点 ,证明直线
,证明直线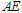 与
与 轴相交于定点
轴相交于定点 ;
;
(3)在(2)的条件下,过点 的直线与椭圆
的直线与椭圆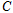 交于
交于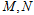 两点,求
两点,求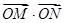 的取值范围.
的取值范围.
已知抛物线
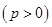 上点
上点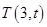 到焦点
到焦点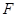 的距离为4.
的距离为4.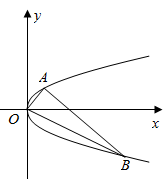
(1)求 ,
, 值;
值;
(2)设 ,
,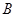 是抛物线上分别位于
是抛物线上分别位于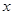 轴两侧的两个动点,且
轴两侧的两个动点,且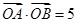 (其中
(其中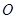 为坐标原点).求证:直线
为坐标原点).求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
设函数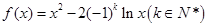 ,
,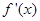 表示
表示 的导函数.
的导函数.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)当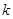 为偶数时,若函数
为偶数时,若函数 的图象恒在函数
的图象恒在函数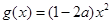 的上方,求实数
的上方,求实数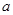 的取值范围;
的取值范围;
(3)当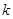 为奇数时,设
为奇数时,设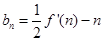 ,数列
,数列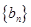 的前
的前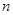 项和为
项和为 ,证明不等式
,证明不等式 对一切正整数
对一切正整数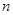 均成立,并比较
均成立,并比较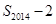 与
与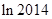 的大小.
的大小.
已知抛物线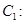
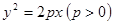 的焦点为
的焦点为 ,抛物线上存在一点
,抛物线上存在一点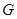 到焦点的距离为
到焦点的距离为 ,且点
,且点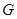 在圆
在圆
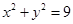 上.
上.
(1)求抛物线 的方程;
的方程;
(2)已知椭圆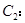
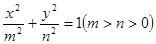 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为 .直线
.直线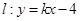 交椭圆
交椭圆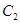 于
于 、
、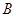 两个不同的点,若原点
两个不同的点,若原点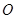 在以线段
在以线段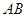 为直径的圆的外部,求
为直径的圆的外部,求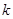 的取值范围.
的取值范围.
已知椭圆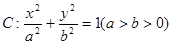 的离心率为
的离心率为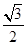 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线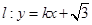 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
已知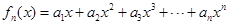 ,且
,且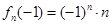 ,
, 1,2,3,….
1,2,3,….
(1)求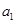 ,
, ,
,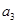 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)当 且
且 时,证明:对任意
时,证明:对任意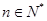 都有
都有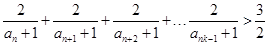 成立.
成立.
在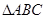 中,角
中,角 ,
,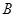 ,
,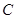 所对的边分别为
所对的边分别为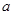 ,
,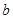 ,
, ,
,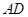 为边
为边 上的高,已知
上的高,已知 ,
, .
.
(1)若 ,求
,求 ;
;
(2)求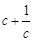 的最大值.
的最大值.
微信是现代生活进行信息交流的重要工具,据统计,某公司 名员工中
名员工中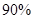 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有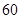 人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于
人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于 岁)和中年(年龄不小于
岁)和中年(年龄不小于 岁)两个阶段,使用微信的人中
岁)两个阶段,使用微信的人中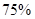 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中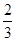 是青年人.
是青年人.
(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出 列联表;
列联表;
| |
青年人 |
中年人 |
合计 |
| 经常使用微信 |
|
|
|
| 不经常使用微信 |
|
|
|
| 合计 |
|
|
|
(Ⅱ)由列联表中所得数据,是否有 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?
(Ⅲ)采用分层抽样的方法从“经常使用微信”的人中抽取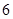 人,从这
人,从这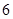 人中任选
人中任选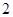 人,求事件
人,求事件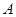 “选出的
“选出的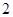 人均是青年人”的概率.
人均是青年人”的概率.
附: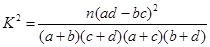
 |
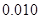 |
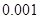 |
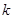 |
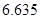 |
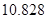 |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 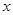 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间  (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(1)求出 关于
关于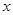 的线性回归方程
的线性回归方程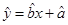 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;

(2)试预测加工 个零件需要多少小时?
个零件需要多少小时?
(注: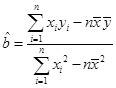 ,
, ,
, ,
,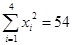 )
)