设椭圆C1: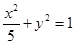 的右焦点为F,P为椭圆上的一个动点.
的右焦点为F,P为椭圆上的一个动点.
(1)求线段PF的中点M的轨迹C2的方程;
(2)过点F的直线l与椭圆C1相交于点A、D,与曲线C2顺次相交于点B、C,当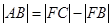 时,求直线l的方程.
时,求直线l的方程.
在数列{an}中, ,
,
 ,
,
(1)求数列 的通项公式
的通项公式
(2)设 (
( ),记数列
),记数列 的前k项和为
的前k项和为 ,求
,求 的最大值.
的最大值.
已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线 没有公共点,求
没有公共点,求 的最大值.
的最大值.
巳知椭圆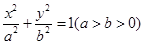 的离心率是
的离心率是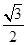 .
.
⑴若点P(2,1)在椭圆上,求椭圆的方程;
⑵若存在过点A(1,0)的直线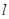 ,使点C(2,0)关于直线
,使点C(2,0)关于直线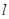 的对称点在椭圆上,求椭圆的焦距的取值范围.
的对称点在椭圆上,求椭圆的焦距的取值范围.
巳知椭圆 的离心率是
的离心率是 .
.
⑴若点P(2,1)在椭圆上,求椭圆的方程;
⑵若存在过点A(1,0)的直线 ,使点C(2,0)关于直线
,使点C(2,0)关于直线 的对称点在椭圆上,求椭圆的焦距的取值范围.
的对称点在椭圆上,求椭圆的焦距的取值范围.
已知函数 是定义域为
是定义域为 的偶函数.当
的偶函数.当 时,
时, 若关于
若关于 的方程
的方程
 有且只有7个不同实数根,则
有且只有7个不同实数根,则 的值是.
的值是.
A.(坐标系与参数方程)已知直线的参数方程为 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为 (
( 为参数),则圆心
为参数),则圆心 到直线的距离为_________.
到直线的距离为_________.
B.(几何证明选讲)如右图,直线 与圆
与圆 相切于点
相切于点 ,割线
,割线 经过圆心
经过圆心 ,弦
,弦 ⊥
⊥ 于点
于点 ,
, ,
, ,则
,则 _________.
_________.
C.(不等式选讲)若存在实数 使
使 成立,则实数
成立,则实数
的取值范围是_________.
已知椭圆 的左右焦点分别为
的左右焦点分别为 、
、 ,短轴两个端点为
,短轴两个端点为 、
、 ,且四边形
,且四边形 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆方程;
(2)若 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点 ,证明:
,证明: 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线 的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
已知函数 ,
, .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为 ,其中
,其中 ,求
,求 的最小值.
的最小值.
已知 (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.
抛物线 ,直线
,直线 过抛物线
过抛物线 的焦点
的焦点 ,交
,交 轴于点
轴于点 .
.
(1)求证: ;
;
(2)过 作抛物线
作抛物线 的切线,切点为
的切线,切点为 (异于原点),
(异于原点),
(i) 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ii) 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
已知函数 图像上一点
图像上一点 处的切线方程为
处的切线方程为 (1)求
(1)求 的值;(2)若方程
的值;(2)若方程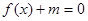 在区间
在区间 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令 如果
如果 的图像与
的图像与 轴交于
轴交于 两点,
两点,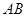 的中点为
的中点为 ,求证:
,求证: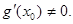
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点. 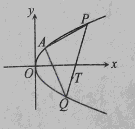
(1)若直线PQ过定点 ,求点A的坐标;
,求点A的坐标;
(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.
如图,椭圆 的中心为原点
的中心为原点 ,长轴在
,长轴在 轴上,离心率
轴上,离心率 ,又椭圆
,又椭圆 上的任一点到椭圆
上的任一点到椭圆 的两焦点的距离之和为
的两焦点的距离之和为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若平行于 轴的直线
轴的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 、
、 ,过
,过 、
、 两点作圆心为
两点作圆心为 的圆,使椭圆
的圆,使椭圆 上的其余点均在圆
上的其余点均在圆 外.求
外.求 的面积
的面积 的最大值.
的最大值.
已知 .
.
(1)求函数 在
在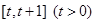 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数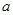 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有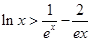 成立.
成立.