吉林省长春市高中毕业班第一次调研测试理科试卷
已知集合 ,集合N="{" x|lg(3-x)>0},则
,集合N="{" x|lg(3-x)>0},则 ( )
( )
| A.{x|2<x<3} | B.{x|1<x<3} | C.{x|1<x<2} | D. |
实数x,y满足 ,若函数z=x+y的最大值为4,则实数a的值为( )
,若函数z=x+y的最大值为4,则实数a的值为( )
| A.2 | B.3 | C. |
D.4 |
已知三条不重合的直线m,n,l 和两个不重合的平面α,β ,下列命题正确的是:( )
A.若m//n,n α,则m//α α,则m//α |
B.若α⊥β, α β="m," n⊥m ,则n⊥α. β="m," n⊥m ,则n⊥α. |
| C.若l⊥n ,m⊥n,则l//m |
| D.若l⊥α,m⊥β, 且l⊥m ,则α⊥β |
已知双曲线 的右顶点、左焦点分别为A、F,点B(0,-b),
的右顶点、左焦点分别为A、F,点B(0,-b),
若 ,则双曲线的离心率值为( )
,则双曲线的离心率值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
若函数y=f(x)图象上的任意一点p的坐标(x,y)满足条件|x|≥|y|,则称函数具有性质S,那么下列函数中具有性质S的是( )
| A.f(x)=tanx | B. -1 -1 |
| C.f(x)=sinx | D.f(x)= ln(x+1) |
已知三棱柱ABC-A1B1C1底面是边长为 的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12
的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12 ,则该三棱柱的体积为.
,则该三棱柱的体积为.
定义[x]表示不超过x的最大整数,例如:[1.5]=1,[-1.5]=-2,若f(x)=sin(x-[x]),则下列结论中
①y=f(x)是奇是函数②.y=f(x)是周期函数,周期为2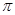 ③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.
③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.
已知向量 ,设函数
,设函数 .
.
(1).求函数f(x)的最小正周期;
(2).已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1, ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点,
(1).求证:D1E⊥A1D;
(2).在线段AB上是否存在点M,使二面角D1-MC-D的大小为 ?,若存在,求出AM的长,若不存在,说明理由
?,若存在,求出AM的长,若不存在,说明理由
已知椭圆 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(1).当p+q≤0时,求椭圆的离心率的取值范围;
(2).若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时, 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.
已知函数 ,
, .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为 ,其中
,其中 ,求
,求 的最小值.
的最小值.
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点E.
(1).求证:E为AB的中点;
(2).求线段FB的长.
以直角坐标系的原点为极点O, 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.

 的焦点到准线的距离是( )
的焦点到准线的距离是( )

 中,
中, 前三项和为
前三项和为 ,则公比q的值是( )
,则公比q的值是( )
 ,运算原理如图所示,则式子
,运算原理如图所示,则式子 的值为( )
的值为( )


 =___
=___ ,圆
,圆 ,
, ,若圆C2平分圆C1的周长,则
,若圆C2平分圆C1的周长,则 的所有项的和为.
的所有项的和为. 的前n项和为
的前n项和为 ,且
,且 ,
, 成等比数列,求正整数n的值.
成等比数列,求正整数n的值. M时,证明:2|a+b|<|4+ab|.
M时,证明:2|a+b|<|4+ab|. 粤公网安备 44130202000953号
粤公网安备 44130202000953号