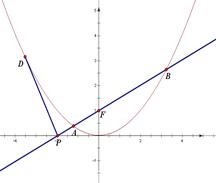
抛物线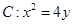 ,直线
,直线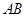 过抛物线
过抛物线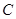 的焦点
的焦点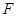 ,交
,交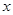 轴于点
轴于点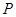 .
.
(1)求证: ;
;
(2)过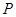 作抛物线
作抛物线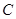 的切线,切点为
的切线,切点为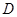 (异于原点),
(异于原点),
(i)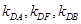 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ii) 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
相关知识点
推荐套卷
抛物线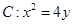 ,直线
,直线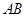 过抛物线
过抛物线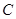 的焦点
的焦点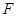 ,交
,交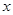 轴于点
轴于点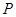 .
.
(1)求证: ;
;
(2)过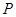 作抛物线
作抛物线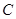 的切线,切点为
的切线,切点为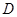 (异于原点),
(异于原点),
(i)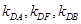 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ii) 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.