河南中原名校高三下学期第二次联考理科数学试卷
下列命题正确的个数是( )
①“在三角形ABC中,若 ,则
,则 ”的逆命题是真命题;②命题
”的逆命题是真命题;②命题 或
或 ,命题
,命题 则
则 是
是 的必要不充分条件;③“
的必要不充分条件;③“ ”的否定是“
”的否定是“ ”;④若随机变量
”;④若随机变量 ,则
,则 ⑤回归分析中,回归方程可以是非线性方程.
⑤回归分析中,回归方程可以是非线性方程.
| A.1 | B.2 | C.3 | D.4 |
一个算法的程序框图如右图所示,若该程序输出的P位于区间 内,则判断框内应填入的条件是( )
内,则判断框内应填入的条件是( ) 
A. |
B. |
C. |
D. |
已知双曲线 ,以右顶点为圆心,实半轴长为半径的圆被双曲线的一条渐近线分为弧长为1:2的两部分,则双曲线的离心率为( )
,以右顶点为圆心,实半轴长为半径的圆被双曲线的一条渐近线分为弧长为1:2的两部分,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
在三角形ABC中, 的平分线交BC于D,AB="4,"
的平分线交BC于D,AB="4,"  ,则AD的长为( )
,则AD的长为( )
A. |
B. |
C. |
D. |
已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA="PD=AB=2,"  若点P,A,B,C,D都在同一球面上,则此球的表面积等于( )
若点P,A,B,C,D都在同一球面上,则此球的表面积等于( )
A. |
B. |
C. |
D. |
将数字1,2,3,4填入右侧表格内,要求每行、每列的数字互不相同,如图所示,则不同的填表方式共有( )种.
| 1 |
2 |
3 |
4 |
| 4 |
3 |
1 |
2 |
| 2 |
1 |
4 |
3 |
| 3 |
4 |
2 |
1 |
A.432 B.576 C.720 D.864
已知函数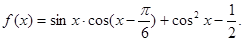
(1)求函数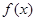 的最大值,并写出
的最大值,并写出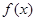 取最大值
取最大值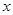 时的取值集合;
时的取值集合;
(2)在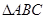 中,角
中,角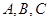 的对边分别为
的对边分别为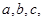 ,若
,若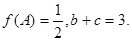 求
求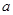 的最小值.
的最小值.
某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的被淘汰.若有500人参加测试,学生成绩的频率分布直方图如图.
(1)求获得参赛资格的人数;
(2)根据频率直方图,估算这500名学生测试的平均成绩;
(3)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响.已知他连续两次答错的概率为 ,求甲在初赛中答题个数
,求甲在初赛中答题个数 的分布列及数学期望
的分布列及数学期望 .
.
如图,在直角梯形ABCP中,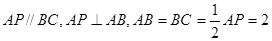 ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为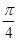 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.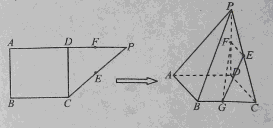
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点. 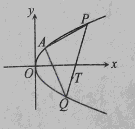
(1)若直线PQ过定点 ,求点A的坐标;
,求点A的坐标;
(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.
已知函数 图像上一点
图像上一点 处的切线方程为
处的切线方程为 (1)求
(1)求 的值;(2)若方程
的值;(2)若方程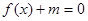 在区间
在区间 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令 如果
如果 的图像与
的图像与 轴交于
轴交于 两点,
两点,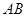 的中点为
的中点为 ,求证:
,求证: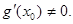
如图,在锐角三角形ABC中,D 为C在AB上的射影,E 为D在BC上的射影,F为DE上一点,且满足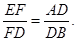
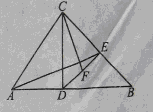
(1)证明: (2)若AD=2,CD=3.DB=4,求
(2)若AD=2,CD=3.DB=4,求 的值.
的值.
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,两种坐标系取相同单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同单位长度.已知曲线 过点
过点 的直线
的直线 的参数方程为
的参数方程为 (t为参数). (1)求曲线C与直线
(t为参数). (1)求曲线C与直线 的普通方程;(2)设曲线C经过伸缩变换
的普通方程;(2)设曲线C经过伸缩变换 得到曲线
得到曲线 ,若直线
,若直线 与曲线
与曲线 相切,求实数
相切,求实数 的值.
的值.
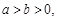 集合
集合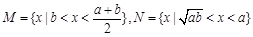 ,则集合
,则集合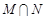 等于( )
等于( )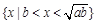
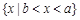
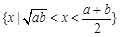
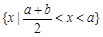
 为纯虚数,
为纯虚数, 是实数,那么
是实数,那么 ( )
( )








 为定义在R上的偶函数,且当
为定义在R上的偶函数,且当 时,
时, 则下列选项正确的是( )
则下列选项正确的是( )



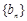 为等差数列,
为等差数列,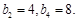 数列
数列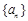 满足
满足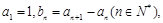 则
则 ( )
( ) 的导函数为
的导函数为 ,且
,且 ,
, 设
设 是方程
是方程 的两根,则
的两根,则 的取值范围是( )
的取值范围是( )



 满足
满足 ,若
,若 的最大值为
的最大值为 则
则
 则
则 的展开式中的常数项是
的展开式中的常数项是 (用数字作答)
(用数字作答) 分别是椭圆的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则
分别是椭圆的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则 的余弦值是
的余弦值是
 存在零点,且对任意
存在零点,且对任意 都满足
都满足 若关于
若关于 的方程
的方程 恰有三个不同的根,则实数
恰有三个不同的根,则实数 的取值范围是
的取值范围是
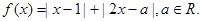 (1)当
(1)当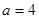 时,求不等式
时,求不等式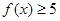 的解集;(2)若
的解集;(2)若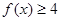 对
对 恒成立,求
恒成立,求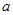 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号