四川省“联测促改”(一)理科数学试卷
“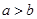 ”是“
”是“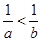 ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要的条件 |
编号为1,2,3,4,5,6的六个同学排成一排,3、4号两位同学相邻,不同的排法( )
| A.60种 | B.120种 | C.240种 | D.480种 |
设a,b为两条不同的直线, 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )
| A.若a∥α,α⊥β,则a∥β | B.若a∥b,a⊥β,则b⊥β |
| C.若a∥α,b∥α,则a∥b | D.若a⊥b,a∥α,则b⊥α |
已知△ABC的周长为 ,且
,且 .若△ABC的面积为
.若△ABC的面积为 ,则角C的大小为( )
,则角C的大小为( )
| A.30° | B.60° | C.90° | D.120° |
过抛物线 的焦点作直线l交抛物线于A,B两点,分别过A,B作抛物线的切线
的焦点作直线l交抛物线于A,B两点,分别过A,B作抛物线的切线 ,则
,则 与
与 的交点P的轨迹方程是( )
的交点P的轨迹方程是( )
A. |
B. |
C. |
D. |
如图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 .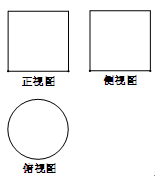
在直角坐标系中,定义两点 之间的“直角距离”为
之间的“直角距离”为 .现有下列命题:
.现有下列命题:
①已知P (1,3),Q( ) (
) ( ),则d(P,Q)为定值;
),则d(P,Q)为定值;
②原点O到直线 上任一点P的直角距离d (O, P)的最小值为
上任一点P的直角距离d (O, P)的最小值为 ;
;
③若 表示P、Q两点间的距离,那么
表示P、Q两点间的距离,那么 ;
;
④设A(x,y)且 ,若点A是在过P (1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.
,若点A是在过P (1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.
其中的真命题是 .(写出所有真命题的序号)
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,设 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求 的分布列和期望.
的分布列和期望.
学校餐厅每天供应500名学生用餐,每星期一有A, B两种菜可供选择。调查表明,凡是在这星期一选A菜的,下星期一会有 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.
⑴试用 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由;
⑵若第一个星期一选A种菜的有200人,那么第10个星期一选A种菜的大约有多少人?
已知四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD= AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.
⑴确定Q的位置;
⑵求二面角Q-BD-C的平面角的余弦值.
巳知椭圆 的离心率是
的离心率是 .
.
⑴若点P(2,1)在椭圆上,求椭圆的方程;
⑵若存在过点A(1,0)的直线 ,使点C(2,0)关于直线
,使点C(2,0)关于直线 的对称点在椭圆上,求椭圆的焦距的取值范围.
的对称点在椭圆上,求椭圆的焦距的取值范围.
 ,则
,则 ( )
( )



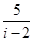 的共扼复数是( )
的共扼复数是( )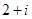
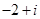
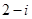
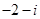
 ( )
( ) 的零点个数为( )
的零点个数为( ) ,则输出的结果是( )
,则输出的结果是( )




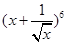 的展开式中的常数项是 .
的展开式中的常数项是 .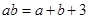 ,则ab的最小值为 .
,则ab的最小值为 .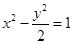 的右焦点作直线l交双曲线于A、B两点,若满足
的右焦点作直线l交双曲线于A、B两点,若满足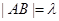 的直线l共有3条,则实数
的直线l共有3条,则实数 .
. ,函数
,函数 .
. ,x为某三角形的内角,求
,x为某三角形的内角,求 时x的值;
时x的值; ,当函数
,当函数 取最大值时,求cos2x的值.
取最大值时,求cos2x的值.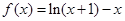 .
.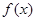 在
在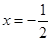 处的切线方程;
处的切线方程;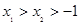 时,求证:
时,求证: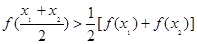 ;
;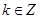 ,且
,且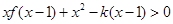 对任意
对任意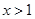 恒成立,求k的最大值.
恒成立,求k的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号