为了解某校学生参加某项测试的情况，从该校学生中随机抽取了6位同学，这6位同学的成绩(分数)如茎叶图所示.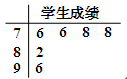
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况，设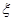
为这两位同学中成绩低于平均分的人数，求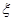的分布列和期望.
＞106的最小正整数,写出算法的程序并画出程序框图.推荐套卷
为了解某校学生参加某项测试的情况，从该校学生中随机抽取了6位同学，这6位同学的成绩(分数)如茎叶图所示.
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况，设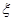为这两位同学中成绩低于平均分的人数，求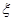的分布列和期望.
粤公网安备 44130202000953号