已知四棱锥P-ABCD中，PB⊥平面ABCD，底面ABCD是直角梯形,∠ABC=∠BCD=90°，PB=BC=CD=
AB.Q是PC上的一点，且PA∥平面QBD.
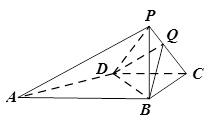
⑴确定Q的位置;
⑵求二面角Q-BD-C的平面角的余弦值.
是公比为
的等比数列，推导
项公式.
满足：
，
.
的各项均为正数，
为其前
项和，若
，
，求
，
，
，求B及S
.
中，
的对边分别为
，若
.
；
的值；
，求△
的面积
满足
，且
，
与
的夹角为
.
的最大值及最小值.相关知识点
推荐套卷
已知四棱锥P-ABCD中，PB⊥平面ABCD，底面ABCD是直角梯形,∠ABC=∠BCD=90°，PB=BC=CD=AB.Q是PC上的一点，且PA∥平面QBD.
⑴确定Q的位置;
⑵求二面角Q-BD-C的平面角的余弦值.
粤公网安备 44130202000953号