甘肃省张掖市高三第三次诊断考试理科数学试卷
我校要从4名男生和2名女生中选出2人担任 禽流感防御宣传工作,则在选出的宣传者中男、女都有的概率为( ).
禽流感防御宣传工作,则在选出的宣传者中男、女都有的概率为( ).
A.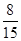 |
B. |
C.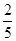 |
D. |
设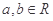 ,则
,则 是
是 的( ).
的( ).
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 为执行如图所示的程序框图输出的结果,则二项式
为执行如图所示的程序框图输出的结果,则二项式 的展开式中含
的展开式中含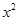 项的系数是( ).
项的系数是( ).
| A.192 | B.32 | C.96 | D.-192 |
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积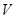 为( ).
为( ).
A. |
B. |
C. |
D. |
如图, ,
, 是双曲线
是双曲线 :
: 与椭圆
与椭圆 的公共焦点,点
的公共焦点,点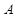 是
是 ,
, 在第一象限的公共点.若|F1F2|=|F1A|,则
在第一象限的公共点.若|F1F2|=|F1A|,则 的离心率是( ).
的离心率是( ).
A. |
B.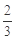 |
C. |
D. |
已知定义在 上的函数
上的函数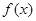 是奇函数且满足
是奇函数且满足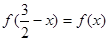 ,
,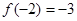 ,数列
,数列 满足
满足 ,且
,且 ,(其中
,(其中 为
为 的前
的前 项和),则
项和),则 ( ).
( ).
A. |
B. |
C. |
D. |
下列结论中正确命题的序号是(写出所有正确命题的序号).
①积分 的值为2;②若
的值为2;②若 ,则
,则 与
与 的夹角为钝角;③若
的夹角为钝角;③若 ,则不等式
,则不等式 成立的概率是
成立的概率是 ;④函数
;④函数 的最小值为2.
的最小值为2.
甲、乙、丙、丁4名同学被随机地分到 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学.
(1)求甲、乙两人都被分到 社区的概率;
社区的概率;
(2)求甲、乙两人不在同一个社区的概率;
(3)设随机变量 为四名同学中到
为四名同学中到 社区的人数,求
社区的人数,求 的分布列和
的分布列和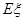 的值.
的值.
如图,在长方体 中,
中, 点
点 在棱
在棱 上.
上.
(1)求异面直线 与
与 所成的角;
所成的角;
(2)若二面角 的大小为
的大小为 ,求点
,求点 到平面
到平面 的距离.
的距离.
已知椭圆 的离心率为
的离心率为 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 与椭圆
与椭圆 相交于
相交于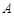 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
已知 .
.
(1)求函数 在
在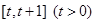 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数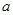 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有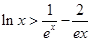 成立.
成立.
如图,已知 点在圆
点在圆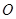 直径
直径 的延长线上,
的延长线上, 切圆
切圆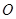 于
于 点,
点, 是
是 的平分线交
的平分线交 于点
于点 ,交
,交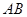 于
于 点.
点.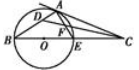
(1)求 的度数;(2)若
的度数;(2)若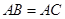 ,求
,求 .
.
在平面直角坐标系中,已知直线的参数方程是(为参数);以为极点,轴正半轴为极轴的极坐标系中,圆的极坐标方程为.
(1)写出直线的普通方程与圆的直角坐标方程;
(2)由直线上的点向圆引切线,求切线长的最小值.
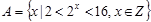 ,
, ,则
,则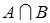 中元素个数为( ).
中元素个数为( ). ,其中
,其中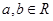 ,则
,则 =( ).
=( ). +i
+i


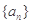 中,
中,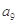 =
= ,则数列
,则数列 =( ).
=( ). 的最小正周期为( ).
的最小正周期为( ).
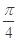
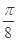

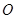 是坐标原点,点
是坐标原点,点 ,若点
,若点 为平面区域
为平面区域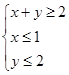 上的一个动点,则
上的一个动点,则 的取值范围是( ).
的取值范围是( ).


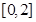
 关于直线
关于直线 对称,则由点
对称,则由点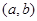 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( ) 中,角
中,角 、
、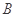 、
、 的对边分别是
的对边分别是 、
、 、
、 ,若
,若 ,
, ,
, ,则角
,则角 在点
在点 处的切线与两坐标轴围成三角形的面积为
处的切线与两坐标轴围成三角形的面积为 ,则
,则 ________.
________.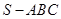 中,
中,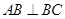 ,
, ,
,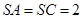 ,二面角
,二面角 的余弦值是
的余弦值是 ,若
,若 都在同一球面上,则该球的表面积是.
都在同一球面上,则该球的表面积是. 的最小正周期为
的最小正周期为 .
. 时,求函数
时,求函数 的最小值;
的最小值; ,若
,若 ,且
,且 ,求
,求 的值.
的值.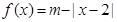 ,m∈R,且
,m∈R,且 的解集为
的解集为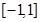 .
.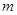 的值;
的值;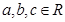 +,且
+,且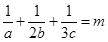 ,求
,求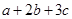 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号