A.(坐标系与参数方程)已知直线的参数方程为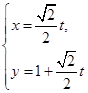 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为 (
( 为参数),则圆心
为参数),则圆心 到直线的距离为_________.
到直线的距离为_________.
B.(几何证明选讲)如右图,直线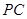 与圆
与圆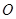 相切于点
相切于点 ,割线
,割线 经过圆心
经过圆心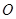 ,弦
,弦 ⊥
⊥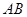 于点
于点 ,
,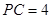 ,
,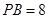 ,则
,则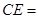 _________.
_________.
C.(不等式选讲)若存在实数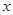 使
使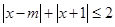 成立,则实数
成立,则实数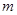
的取值范围是_________.
推荐套卷
A.(坐标系与参数方程)已知直线的参数方程为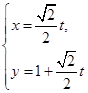 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为 (
( 为参数),则圆心
为参数),则圆心 到直线的距离为_________.
到直线的距离为_________.
B.(几何证明选讲)如右图,直线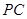 与圆
与圆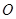 相切于点
相切于点 ,割线
,割线 经过圆心
经过圆心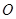 ,弦
,弦 ⊥
⊥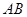 于点
于点 ,
,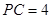 ,
,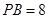 ,则
,则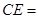 _________.
_________.
C.(不等式选讲)若存在实数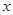 使
使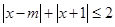 成立,则实数
成立,则实数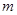
的取值范围是_________.