口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为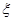 .
.
(1)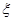 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量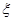 的期望
的期望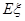 .
.
相关知识点
推荐套卷
口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为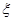 .
.
(1)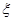 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量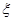 的期望
的期望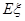 .
.