(本小题满分14分)已知直线l: 与双曲线C:
与双曲线C: (
( )相交于B、D两点,且BD的中点为M(1,3).
)相交于B、D两点,且BD的中点为M(1,3).
(1)求双曲线C的离心率;
(2)设双曲线C的右顶点为A,右焦点为F, ,试判断△ABD是否为直角三角形,并说明理由.
,试判断△ABD是否为直角三角形,并说明理由.
(本小题12分)第(1)小题5分,第(2)题7分
已知中心在原点 ,左焦点为
,左焦点为 的椭圆C的左顶点为
的椭圆C的左顶点为 ,上顶点为
,上顶点为 ,
, 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆C的方程;
(2)若椭圆 方程为:
方程为: (
( ),椭圆
),椭圆 方程为:
方程为: (
( ,且
,且 ),则称椭圆
),则称椭圆 是椭圆
是椭圆 的
的 倍相似椭圆.已知
倍相似椭圆.已知 是椭圆C的
是椭圆C的 倍相似椭圆,若椭圆C的任意一条切线
倍相似椭圆,若椭圆C的任意一条切线 交椭圆
交椭圆 于两点
于两点 、
、 ,试求弦长
,试求弦长 的取值范围.
的取值范围.
(本小题满分12分,(1)小问4分,(2)小问8分)
已知椭圆 :
: 的离心率为
的离心率为 ,且椭圆上一点
,且椭圆上一点 与椭圆的两个焦点
与椭圆的两个焦点 ,
, 满足
满足 .
.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于
交于 ,
, 两点,且以线段
两点,且以线段 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,求
,求 面积的最大值.
面积的最大值.
已知椭圆 的左右焦点分别为
的左右焦点分别为 ,
, 为半焦距,
为半焦距,
(1)求椭圆离心率 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为 ,以
,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,圆
,圆 与
与 轴的右交点为
轴的右交点为 ,过点
,过点 作倾斜角不为
作倾斜角不为 直线
直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若 ,求直线
,求直线 被圆
被圆 截得的弦长
截得的弦长 的取值范围。
的取值范围。
(本小题12分)如图所示,在平面直角坐标系 中,过椭圆
中,过椭圆 内一点
内一点
 的一条直线与椭圆交于点
的一条直线与椭圆交于点 ,且
,且 ,其中
,其中 为常数.
为常数.
(1)求椭圆 的离心率;
的离心率;
(2)当点 恰为椭圆的右顶点时,试确定对应
恰为椭圆的右顶点时,试确定对应 的值;
的值;
(3)当 时,求直线
时,求直线 的斜率.
的斜率.
(本小题满分12分)已知点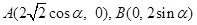 (
( )为平面直角坐标系
)为平面直角坐标系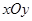 中的点,点S为线段AB的中点,当
中的点,点S为线段AB的中点,当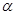 变化时,点S形成轨迹
变化时,点S形成轨迹 .
.
(1)求S点的轨迹 的方程;
的方程;
(2)若点M的坐标为 ,是否存在直线
,是否存在直线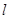 交S点的轨迹
交S点的轨迹 于P、Q两点,且使点
于P、Q两点,且使点 为
为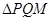 的垂心?若存在,求出直线
的垂心?若存在,求出直线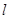 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)已知点 ,
,
 为平面直角坐标系
为平面直角坐标系 中的点,点P为线段EF的中点,当
中的点,点P为线段EF的中点,当 变化时,点P形成的轨迹
变化时,点P形成的轨迹 与x轴交于点A,B(A点在左侧),与y轴正半轴交于点C.
与x轴交于点A,B(A点在左侧),与y轴正半轴交于点C.
(1)求P点的轨迹 的方程;
的方程;
(2)设点M是轨迹 上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
①若D点坐标为 ,求线段CM的长;
,求线段CM的长;
②求证: 为定值.
为定值.
本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
已知数列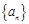 是首项为3,公比为
是首项为3,公比为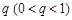 的无穷等比数列,且数列
的无穷等比数列,且数列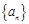 各项的和等于9.对给定的
各项的和等于9.对给定的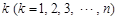 ,设
,设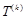 是首项为
是首项为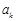 ,公差为
,公差为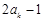 的等差数列.
的等差数列.
(1)求数列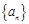 的通项
的通项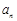 ;
;
(2)求数列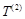 的前10项之和;
的前10项之和;
(3)设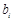 为数列
为数列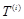 的第
的第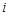 项,
项,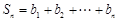 ,求
,求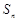 ,并求正整数
,并求正整数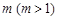 ,使得
,使得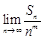 存在且不等于零.
存在且不等于零.
(小题满分12)椭圆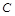 的方程为
的方程为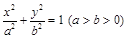 ,
,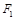 、
、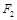 分别是它的左、右焦点,已知椭圆
分别是它的左、右焦点,已知椭圆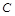 过点
过点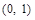 ,且离心率
,且离心率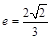 .
.
(1)求椭圆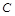 的方程;
的方程;
(2)如图,设椭圆的左、右顶点分别为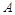 、
、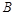 ,直线
,直线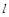 的方程为
的方程为 ,
,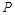 是椭圆上异于
是椭圆上异于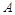 、
、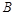 的任意一点,直线
的任意一点,直线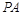 、
、 分别交直线
分别交直线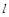 于
于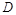 、
、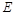 两点,求
两点,求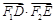 的值;
的值;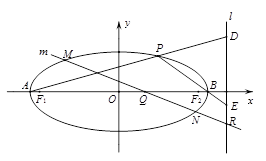
(3)过点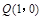 任意作直线
任意作直线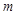 (与
(与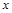 轴不垂直)与椭圆
轴不垂直)与椭圆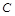 交于
交于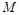 、
、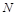 两点,与
两点,与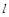 交于
交于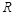 点,
点,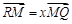 ,
, . 求证:
. 求证: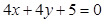 .
.
(本小题满分12分)已知公比为负值的等比数列 中,
中, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了 份,统计结果如下面的图表所示.
份,统计结果如下面的图表所示.
| 组号 |
年龄 分组 |
答对全卷 的人数 |
答对全卷的人数 占本组的概率 |
| 1 |
[20,30) |
28 |
 |
| 2 |
[30,40) |
27 |
0.9 |
| 3 |
[40,50) |
5 |
0.5 |
| 4 |
[50,60] |
 |
0.4 |
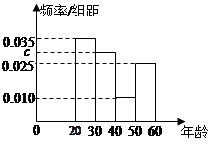
(1)分别求出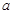 ,
, ,
,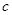 ,
, 的值;
的值;
(2)从第3,4组答对全卷的人中用分层抽样的方法抽取6人,在所抽取的6人中随机抽取2人授予“环
保之星”,记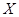 为第3组被授予“环保之星”的人数,求
为第3组被授予“环保之星”的人数,求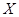 的分布列与数学期望.
的分布列与数学期望.
(本小题满分13分)已知椭圆 :
:
 的焦距为
的焦距为 ,其短轴的两个端点与长轴的一个端点构成正三角形.
,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆 的标准方程;
的标准方程;
(2)设 为椭圆
为椭圆 的左焦点,
的左焦点, 为直线
为直线 上任意一点,过
上任意一点,过 作
作 的垂线交椭圆
的垂线交椭圆 于点
于点 ,
, ,
,
①证明: 平分线段
平分线段 (其中
(其中 为坐标原点),
为坐标原点),
②当 值最小时,求点
值最小时,求点 的坐标.
的坐标.
(本小题满分13分)某批产品成箱包装,每箱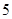 件.一用户在购进该批产品前先取出
件.一用户在购进该批产品前先取出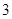 箱,设取出的
箱,设取出的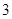 箱中,第一,二,三箱中分别有
箱中,第一,二,三箱中分别有 件,
件,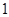 件,
件, 件二等品,其余为一等品.
件二等品,其余为一等品.
(1)在取出的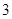 箱中,若该用户从第三箱中有放回的抽取
箱中,若该用户从第三箱中有放回的抽取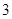 次(每次一件),求恰有两次抽到二等品的概率;
次(每次一件),求恰有两次抽到二等品的概率;
(2)在取出的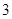 箱中,若该用户再从每箱中任意抽取
箱中,若该用户再从每箱中任意抽取 件产品进行检验,用
件产品进行检验,用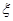 表示抽检的
表示抽检的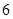 件产品中二等品的件数,求
件产品中二等品的件数,求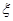 的分布列及数学期望.
的分布列及数学期望.
(本小题满分13分)已知函数


 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函
,纵坐标不变,得到函
数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值.
上的最小值.