已知函数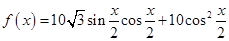 .
.
(Ⅰ)求函数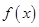 的最小正周期;
的最小正周期;
(Ⅱ)将函数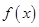 的图象向右平移
的图象向右平移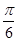 个单位长度,再向下平移
个单位长度,再向下平移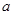 (
(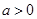 )个单位长度后得到函数
)个单位长度后得到函数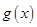 的图象,且函数
的图象,且函数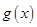 的最大值为2.
的最大值为2.
(ⅰ)求函数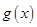 的解析式;
的解析式;
(ⅱ)证明:存在无穷多个互不相同的正整数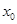 ,使得
,使得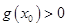 .
.
设椭圆E的方程为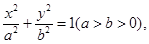 点O为坐标原点,点A的坐标为
点O为坐标原点,点A的坐标为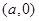 ,点B的坐标为(0,b),点M在线段AB上,满足
,点B的坐标为(0,b),点M在线段AB上,满足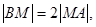 直线OM的斜率为
直线OM的斜率为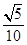 .
.
(Ⅰ)求E的离心率e;
(Ⅱ)设点C的坐标为(0,-b),N为线段AC的中点,证明:MN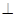 AB.
AB.
某厂商调查甲、乙两种不同型号电视机在10 个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.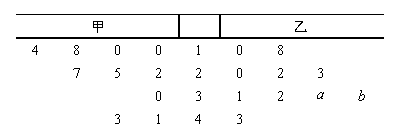
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求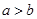 的概率;
的概率;
(3)若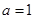 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为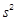 ,根据茎叶图推断
,根据茎叶图推断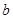 为何值时,
为何值时,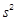 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
(注:方差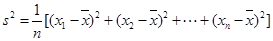 ,其中
,其中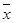 为
为 ,
,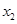 ,…,
,…,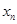 的平均数)
的平均数)
已知椭圆
 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点 ,
, ,若
,若 ,求△
,求△ 的面积.
的面积.
已知椭圆C的中心在原点,焦点y在轴上,焦距为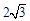 ,且过点M
,且过点M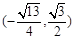 .
.
(1)求椭圆C的方程;
(2)若过点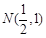 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由.
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由.
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
己知椭圆C: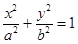 (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线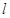 与椭圆C交于不同两点
与椭圆C交于不同两点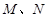 .
.
(1)求椭圆C的方程;
(2)设直线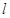 斜率为1,求线段
斜率为1,求线段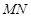 的长;
的长;
(3)设线段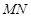 的垂直平分线交
的垂直平分线交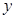 轴于点P(0,y0),求
轴于点P(0,y0),求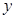 的取值范围.
的取值范围.