已知函数 的定义域为[2,3],值域为[1,4];设
的定义域为[2,3],值域为[1,4];设 .
.
(1)求a,b的值;
(2)若不等式 在
在 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)若 有三个不同的实数解,求实数k的取值范围.
有三个不同的实数解,求实数k的取值范围.
已知函数 .
.
(1)当 ,存在
,存在 (
( 为自然对数的底数),使
为自然对数的底数),使 ,求实数
,求实数 的取值范围;
的取值范围;
(2)当 时,设
时,设 ,在
,在 的图象上是否存在不同的两点
的图象上是否存在不同的两点 ,使得
,使得 ?请说明理由.
?请说明理由.
已知抛物线 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线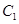 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,与圆
两点,与圆 交于
交于 两点,当
两点,当 时,求
时,求 的取值范围.
的取值范围.
椭圆 的中心在原点,过点
的中心在原点,过点 ,且右焦点
,且右焦点 与圆
与圆 的圆心重合.
的圆心重合.
(1)求椭圆 的方程;
的方程;
(2)过点 的直线
的直线 交椭圆于M、N两点,问是否存在这样的直线
交椭圆于M、N两点,问是否存在这样的直线 ,使得以MN为直径的圆过椭圆的左焦点
,使得以MN为直径的圆过椭圆的左焦点 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由;
的方程;若不存在,请说明理由;
如图,在直三棱柱ABC—A1B1C1中,AC = 3,BC = 4,AB = 5,AA1 = 4.
(1)设 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为 ,求
,求 的值;
的值;
(2)若点D是AB的中点,求二面角D—CB1—B的余弦值.
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系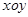 .
.
(1)若最大拱高 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽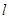 是多少?
是多少?
(2)为了使施工的土方工程量最小,需隧道口截面面积最小. 现隧道口的最大拱高 不小于6米,则应如何设计拱高
不小于6米,则应如何设计拱高 和拱宽
和拱宽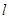 ,使得隧道口截面面积最小?(隧道口截面面积公式为
,使得隧道口截面面积最小?(隧道口截面面积公式为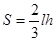 )
)
如图,已知椭圆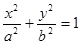 (
(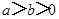 )的左、右焦点为
)的左、右焦点为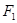 、
、 ,
,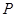 是椭圆上一点,
是椭圆上一点, 在
在 上,且满足
上,且满足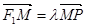 (
(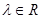 ),
),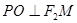 ,
, 为坐标原点.
为坐标原点.
(1)若椭圆方程为 ,且
,且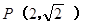 ,求点
,求点 的横坐标;
的横坐标;
(2)若 ,求椭圆离心率
,求椭圆离心率 的取值范围
的取值范围
在极坐标系中,圆 的极坐标方程为
的极坐标方程为 ,已知
,已知 ,
, 为圆
为圆 上一点,求
上一点,求 面积的最小值.
面积的最小值.
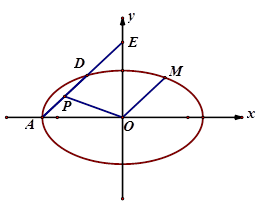
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: 的离心率
的离心率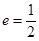 ,左顶点为
,左顶点为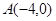 ,过点
,过点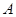 作斜率为
作斜率为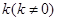 的直线
的直线 交椭圆
交椭圆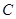 于点
于点 ,交
,交 轴于点
轴于点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知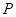 为
为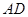 的中点,是否存在定点
的中点,是否存在定点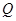 ,对于任意的
,对于任意的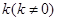 都有
都有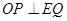 ,若存在,求出点
,若存在,求出点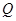 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)若过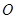 点作直线
点作直线 的平行线交椭圆
的平行线交椭圆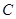 于点
于点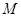 ,求
,求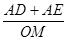 的最小值.
的最小值.