选修4-4:坐标系与参数方程
在极坐标系中,曲线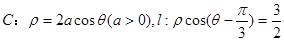 ,曲线C与
,曲线C与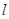 有且仅有一个公共点.
有且仅有一个公共点.
(1)求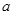 的值;
的值;
(2)O为极点,A,B为C上的两点,且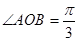 ,求
,求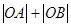 的最大值.
的最大值.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
(Ⅰ)求该校报考飞行员的总人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望.
(双鸭山)已知圆 和圆外一点
和圆外一点 .
.
(1)过点 作圆的割线交圆于
作圆的割线交圆于 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
(2)过点 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为 ,求切线长及
,求切线长及 所在直线的方程.
所在直线的方程.
为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是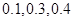 ,第一小组的频数是
,第一小组的频数是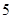 .
.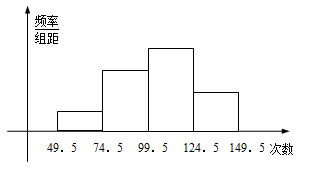
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在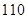 以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多
以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多
少?
已知双曲线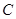 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在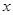 轴上,离心率
轴上,离心率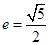 ,虚轴长为2.
,虚轴长为2.
(1)求双曲线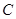 的标准方程;
的标准方程;
(2)若直线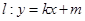 与双曲线
与双曲线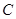 相交于
相交于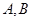 两点,(
两点,(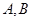 均异于左、右顶点),且以
均异于左、右顶点),且以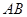 为直径的圆过双曲线
为直径的圆过双曲线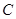 的左顶点
的左顶点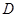 ,求证:直线
,求证:直线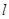 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
在平面直角坐标系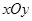 中,已知椭圆
中,已知椭圆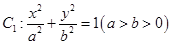 的左焦点为
的左焦点为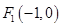 ,且椭圆上的点到焦点的距离的最小值为
,且椭圆上的点到焦点的距离的最小值为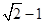 .
.
(1)求椭圆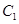 的方程;
的方程;
(2)设直线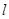 过点
过点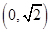 且与椭圆
且与椭圆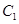 相切,求直线
相切,求直线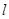 的方程.
的方程.
已知双曲线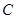 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在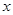 轴上,离心率
轴上,离心率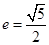 ,虚轴长为2.
,虚轴长为2.
(1)求双曲线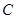 的标准方程;
的标准方程;
(2)若直线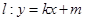 与双曲线
与双曲线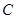 相交于
相交于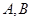 两点,(
两点,(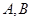 均异于左、右顶点),且以
均异于左、右顶点),且以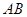 为直径的圆过双曲线
为直径的圆过双曲线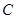 的左顶点
的左顶点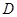 ,求证:直线
,求证:直线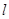 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.