已知函数f(x)= x2﹣lnx+x+1,g(x)=aex+
x2﹣lnx+x+1,g(x)=aex+ +ax﹣2a﹣1,其中a∈R.
+ax﹣2a﹣1,其中a∈R.
(Ⅰ)若a=2,求f(x)的极值点;
(Ⅱ)试讨论f(x)的单调性;
(Ⅲ)若a>0,∀x∈(0,+∞),恒有g(x)≥f′(x)(f′(x)为f(x)的导函数),求a的最小值.
已知抛物线C:x2=2py(p>0)的焦点为F,抛物线上一点A的横坐标为x1(x1>0),过点A作抛物线C的切线l1交x轴于点D,交y轴于点Q,当|FD|=2时,∠AFD=60°.
(1)求证:FD垂直平分AQ,并求出抛物线C的方程;
(2)若B位于y轴左侧的抛物线C上,过点B作抛物线C的切线l2交直线l1于点P,AB交y轴于点(0,m),若∠APB为锐角,求m的取值范围.
已知椭圆C: 的离心率为
的离心率为 ,其中左焦点(﹣2,0).
,其中左焦点(﹣2,0).
(1)求椭圆C的方程;
(2)若直线y=x+m与椭圆C交于不同的两点A,B,求线段AB的最大值.
设定函数f(x)= x3+bx2+cx+d(a>0),且方程f′(x)﹣9x=0的两个根分别为1,4.
x3+bx2+cx+d(a>0),且方程f′(x)﹣9x=0的两个根分别为1,4.
(1)当a=3且曲线y=f(x)过原点时,求f(x)的解析式;
(2)若f(x)在(﹣∞,+∞)无极值点,求a的取值范围.
已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为 ,且
,且 .
.
(1)求此抛物线 的方程;
的方程;
(2)过点 做直线
做直线 交抛物线
交抛物线 于
于 两点,求证:
两点,求证: .
.
已知函数 ,其中
,其中 且
且 .
.
(1)当 时,若
时,若 无解,求
无解,求 的范围;
的范围;
(2)若存在实数 ,
, (
( ),使得
),使得 时,函数
时,函数 的值域都也为
的值域都也为 ,求
,求 的范围.
的范围.
设数列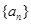 的前
的前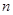 项和为
项和为 ,已知
,已知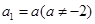 ,
,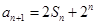 ,
, .
.
(1)设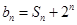 ,求证:数列
,求证:数列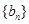 是等比数列;
是等比数列;
(2)若数列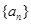 是单调递增数列,求实数
是单调递增数列,求实数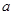 的取值范围.
的取值范围.
已知向量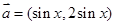 ,
,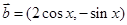 ,函数
,函数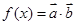 .
.
(1)求函数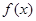 的最小正周期;
的最小正周期;
(2)求函数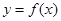 在
在 上的值域.
上的值域.
已知点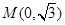 是椭圆
是椭圆 :
: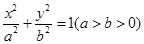 的一个顶点,椭圆
的一个顶点,椭圆 的离心率为
的离心率为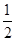 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点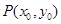 是定点,直线
是定点,直线 :
: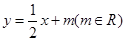 交椭圆
交椭圆 于不同的两点
于不同的两点 ,
, ,记直线
,记直线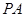 ,
,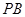 的斜率分别为
的斜率分别为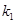 ,
,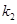 ,求点
,求点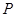 的坐标,使得
的坐标,使得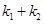 恒为0.
恒为0.
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形, ,
, ,且
,且 ,
, 分别为
分别为 ,
, 的中点.
的中点.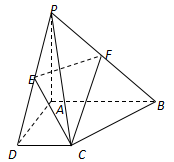
(1)求证: 平面
平面 ;
;
(2)若直线 与平面
与平面 的交点为
的交点为 ,且
,且 ,求截面
,求截面 与底面
与底面 所成锐二面角的大小.
所成锐二面角的大小.