已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(1)当 时,求过点
时,求过点 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;
(2)若 在(0,1)上恒成立,求实数
在(0,1)上恒成立,求实数 的取值范围.
的取值范围.
已知椭圆 与椭圆
与椭圆 :
: 共焦点,并且经过点
共焦点,并且经过点 ,
,
(1)求椭圆 的标准方程;
的标准方程;
(2)在椭圆 上任取两点
上任取两点 ,设
,设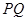 所在直线与
所在直线与 轴交于点
轴交于点 ,点
,点 为点
为点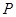 关于轴
关于轴 的对称点,
的对称点,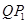 所在直线与
所在直线与 轴交于点
轴交于点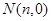 ,探求
,探求 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
已知函数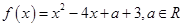
(1)若函数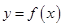 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;
(2) 若函数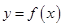 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;
(3)设函数 ,当
,当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使得
,使得 ,求b的取值范围.
,求b的取值范围.
某地区为了了解某地区高中生的身体发育情况,对某一中学的随机抽取的50名学生的体重进行了测量,结果如下:(单位:kg)
42,38,29,36,41,43,54,43,34,44,40,59,39,42,44,50,37,44,45,29,48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,,67,53,49,65,47,54,63,58,43,46,58.
| 分组 |
频数 |
频率 |
频率/组距 |
| [27,32) |
|
0.06 |
|
| [32,37) |
|
0.06 |
|
| [37,42) |
9 |
|
|
| [42,47) |
|
|
0.064 |
| [47,52) |
7 |
|
|
| [52,57) |
5 |
|
|
| [57,62) |
4 |
|
|
| [62,67) |
|
0.06 |
|
(1)若以组距为5,完成下面样本频率分布表:
(2)根据(1)中的频率分布表,画出频率分布直方图;
(3)若本地区学生总人数为3000人,试根据抽样比例,估计本地区学生体重在区间[37,57]内所占的人数约为多少人?
某市电视台在因特网上征集电视节目的现场参与观众,报名的共有12000人,分别来自4个城区,其中东城区2400人,西城区4600人,南城区3800人,北城区1200人,从中抽取60人参加现场节目,应当如何抽取?