高中数学解答题

通过研究学生的行为，心理学家发现，学生的接受能力依赖于教师引入概念和描述问题所用的时间．讲座开始时，学生的兴趣急增；中间有一段不太长的时间，学生的学习兴趣保持较理想的状态，随后学生的学习兴趣开始分散．分析结果和实验表明，用表示学生掌握和接受概念的能力，x表示提出和讲授概念的时间（单位分）可以用下面公式：

（1）开讲后多少分钟，学生的接受能力最强？能持续多长时间？
（2）一个数学难题，需要55的接受能力以及13分钟时间，教师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题？

已知函数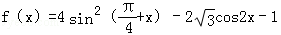，且给定条件p：“”，
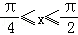（1）求f（x）的最大值及最小值
（2）若又给条件q：“|f（x）﹣m|＜2“且p是q的充分条件，求实数m的取值范围．

如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．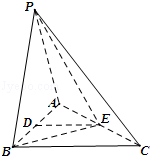

（Ⅰ）求证：DE∥面PBC；
（Ⅱ）求证：AB⊥PE；
（Ⅲ）求三棱锥B﹣PEC的体积．

已知函数．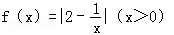
（1）当0＜a＜b且f（a）=f（b）时，①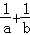求的值；②求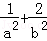的取值范围；
（2）已知函数g（x）的定义域为D，若存在区间[m，n]⊆D，当x∈[m，n]时，g（x）的值域为[m，n]，则称函数g（x）是D上的“保域函数”，区间[m，n]叫做“等域区间”．试判断函数f（x）是否为（0，+∞）上的“保域函数”？若是，求出它的“等域区间”；若不是，请说明理由．

已知函数为偶函数
（1）求实数a的值；
（2）当时，若函数f（x）的值域为[2﹣3m，2﹣3n]，求m，n的值．

已知函数f（x）=（a，b，c∈Z）是奇函数，且f（1）=2，f（2）＜3．
（1）求a，b，c的值．
（2）判断函数f（x）在[1，+∞）上的单调性，并用定义证明你的结论．
（3）解关于t的不等式：f（﹣t²﹣1）+f（|t|+3）＞0．

已知函数f（x）=x³+x．
（1）判断函数f（x）的单调性与奇偶性，（不用证明结论）．
（2）若f（cosθ﹣m）+f（msinθ﹣2）＜0对θ∈R恒成立，求实数m的取值范围．

已知函数f（x）=
（Ⅰ）求f（1），f（﹣3），f（a+1）的值；
（Ⅱ）求函数f（x）的零点．

已知函数．
（1）求函数的极值；
（2）当时，求的最值．

已知函数．
（1）求函数的极值；
（2）当时，求的最值．

已知抛物线的焦点为，抛物线上的点到准线的距离为．
（1）求抛物线的标准方程；
（2）设直线与抛物线的另一交点为，求的值．

已知圆过点，且圆心在直线上．
（1）求圆的方程；
（2）若直线与圆交于两点，当最小时，求直线的方程及的最小值．

已知，，其中．
（1）若，且为真，求的取值范围；
（2）若是的充分不必要条件，求实数的取值范围．

（1）已知，求的值；
（2）．

已知圆的圆心为，，半径为，圆与离心率的椭圆的其中一个公共点为 ，，分别是椭圆的左、右焦点．
（1）求圆的标准方程；
（2）若点的坐标为，试探究直线与圆能否相切，若能，求出椭圆和直线的方程；若不能，请说明理由．