下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x |
3 |
4 |
5 |
6 |
| t |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y= x+
x+ ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为92吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数据:3×2.5+4×3+5×4+6×4.5=66.5)
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| f |
a |
0.2 |
0.45 |
b |
c |
(Ⅰ)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;
(Ⅱ)在(Ⅰ)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
由四个不同的数字1,2,4,x组成无重复数字的三位数.
(1)若x=5,其中能被5整除的共有多少个?
(2)若x=9,其中能被3整除的共有多少个?
(3)若x=0,其中的偶数共有多少个?
(4)若所有这些三位数的各位数字之和是252,求x.
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]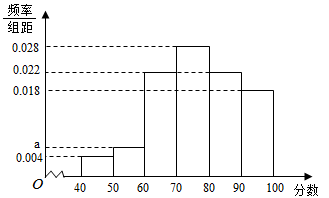
(Ⅰ)求频率分布图中a的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)求出本次评分的众数、中位数、平均数.
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
(1)假设n=2,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
设a>0,f(x)= +
+ 是R上的偶函数.
是R上的偶函数.
(Ⅰ)求a的值;
(Ⅱ)证明f(x)在(0,+∞)上是增函数;
(Ⅲ)解关于x的不等式f(2x﹣1)>e+ .
.
如图,一个圆锥的底面半径为2cm,高为6cm,其中有一个高为xcm的内接圆柱.
(1)试用x表示圆柱的侧面积;
(2)当x为何值时,圆柱的侧面积最大.
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.,当每辆车的月租金定为x元时,租赁公司的月收益为y元,
(1)试写出x,y的函数关系式(不要求写出定义域);
(2)租赁公司某月租出了88辆车,求租赁公司的月收益多少元?
已知函数f(x)=log2x﹣1的定义域为[1,16],函数g(x)=[f(x)]2+af(x2)+2
(1)求函数y=g(x)的定义域;
(2)求函数y=g(x)的最小值;
(3)若函数y=g(x)的图象恒在x轴的上方,求实数a的取值范围.
如图,矩形 ABCD 中,BC=2,AB=1,PA丄平面 ABCD,BE∥PA,BE= PA,F 为PA的中点.
PA,F 为PA的中点.
(I)求证:DF∥平面PEC
(II)记四棱锥C一PABE的体积为V1,三棱锥P﹣ACD的 体积为V2,求 的值.
的值.
如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:
(1)MN∥平面CDD1C1.
(2)平面EBD∥平面FGA.