(本小题满分8分)设 ,动圆P经过点F且和直线
,动圆P经过点F且和直线 相切,记动圆的圆心P的轨迹为曲线W.
相切,记动圆的圆心P的轨迹为曲线W.
(1)求曲线W的方程;
(2)过点F作互相垂直的直线 分别交曲线W与A、B和C、D,求四边形ACBD面积的最小值。
分别交曲线W与A、B和C、D,求四边形ACBD面积的最小值。
(本小题满分8分)如图,已知四棱锥 的
的
底面为直角梯形, ,
, ,
, ,
,
且 ,M是
,M是 的中点。
的中点。
(1) 证明: ;
;
(2) 求异面直线 所成的角的余弦值。
所成的角的余弦值。
(本小题满分8分)嫦娥2号月球卫星接收天线的轴
截面为如图所示的抛物线型,已知接收天线的口径(直径)
为10.8m,深度为1.2m,建立适当的坐标系,求抛物线的
标准方程和焦点坐标。
已知函数 .
.
(Ⅰ)判断f(x)的奇偶性,并说明理由;
(Ⅱ)若方程 有解,求m的取值范围;
有解,求m的取值范围;
(Ⅲ)若函数 ,
, ,对任意
,对任意 都有意义,求
都有意义,求 的取值范围.
的取值范围.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅱ)当AE为何值时,绿地面积最大?
(探究函数 的最小值,并确定相应的x的值,列表如下:
的最小值,并确定相应的x的值,列表如下:
| x |
… |
 |
 |
1 |
 |
2 |
 |
4 |
8 |
16 |
… |
| y |
… |
16.25 |
8.5 |
5 |
 |
4 |
 |
5 |
8.5 |
16.25 |
… |
请观察表中y值随x值变化的特点,完成下列问题:
(Ⅰ)若 ,则
,则
 (请填写“>, ="," <”号);若函数
(请填写“>, ="," <”号);若函数 ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(Ⅱ)当x= 时, ,(x>0)的最小值为 ;
,(x>0)的最小值为 ;
(Ⅲ)试用定义证明 ,(x>0)在区间(0,2)上递减.
,(x>0)在区间(0,2)上递减.
(本小题满分1 2分)
2分)
某商场购进一批单价为16元的日用品,经试 验发现,若按每件
验发现,若按每件 20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
本小题满分1 2分)
2分)
已知函数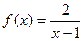 ,
,
(1)利用函数单调性的定义判断函数在区间[2,6]上的单调性;
(2)求函数在区间[2,6]上的最大值和最小值.