抛物线有光学性质:由其焦点射出的光线
 经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然。
经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然。
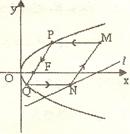
如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴。开
口向右。一光源在点M处,由其发出一条平行于x轴的光线射向
抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点
F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X
轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M。
(1)求抛物线C的方程;
(2)求PQ的长度;
(3)判断四边形MPQN是否为平行四边形,若是请给出证明,若不是请说明理由。