(本小题12分)如图4,四棱锥 中,底面
中,底面 是菱形,其对角线的交点为
是菱形,其对角线的交点为 ,且
,且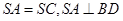 .
.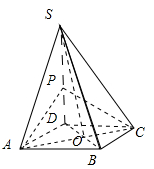
(1)求证: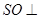 平面
平面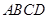 ;
;
(2)设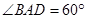 ,
,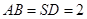 ,
,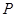 是侧棱
是侧棱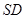 上的一点,且
上的一点,且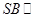 平面
平面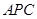 ,求三棱锥
,求三棱锥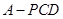 的体积.
的体积.
(本小题10分)如图是一个几何体的主视图和俯视图,
(1)试判断这个几何体是什么几何体;
(2)请画出它的左视图,并求该左视图的面积.
(本小题满分10分)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边长为6,高为4的等腰三角形
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,PA=2 ,BC=CD=2,∠ACB=∠ACD=
,BC=CD=2,∠ACB=∠ACD= .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若侧棱PC上的点F满足PF=7FC,求三棱锥P﹣BDF的体积.
(本小题满分10分)如图, 、
、 是以
是以 为直径的圆上两点,
为直径的圆上两点, ,
, ,
, 是
是 上一点,且
上一点,且 ,将圆沿直径
,将圆沿直径 折起,使点
折起,使点 在平面
在平面 的射影
的射影 在
在 上,已知
上,已知 .
.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分12分)如图四边形ABCD为菱形,G为AC与BD交点, ,
,
(1)证明:平面 平面
平面 ;
;
(2)若 ,
,
 ,令AE与平面ABCD所成角为
,令AE与平面ABCD所成角为 ,且
,且 ,求该四棱锥
,求该四棱锥 的体积.
的体积.
(本小题满分12分) 如图,已知 平面
平面 ,四边形
,四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
(本小题满分12分)如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA,AB=AD=DE= ,M是线段AE上的动点.
,M是线段AE上的动点.
(Ⅰ)试确定点M的位置,使AC//平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE—BCF分成的两部分的体积之比.
已知六棱锥P-ABCDEF,其中底面ABCDEF是正六边形,点P在底面的投影是正六边形的中心,底面边长为2 cm,侧棱长为3 cm,求六棱锥P-ABCDEF的表面积和体积.
如图,是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.
(1)∠DC1D1在图中的度数和它表示的角的真实度数都是45°,对吗?
(2)∠A1C1D的真实度数是60°,对吗?
(3)设BC=1 cm,如果用图示中这样一个装置来盛水,那么最多能盛多少体积的水?
已知某几何体的俯视图是如图所示的矩形,主视图(或称正视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.