(本小题12分) 如图,在边长为12的正方形 中,点B、C在线段AA′上,且AB=3,BC=4.作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1,CC1折叠,使得
中,点B、C在线段AA′上,且AB=3,BC=4.作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1,CC1折叠,使得 与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
(1)在三棱柱ABC-A1B1C1中,求证:AP⊥BC;
(2)在三棱柱ABC-A1B1C1中,连接AQ与A1P,求四面体AA1QP的体积;
(3)在三棱柱ABC- A1B1C1中,求直线 PQ与直线AC所成角的余弦值.
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是()
,则下列结论中错误的是()
A. |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D. 的面积与 的面积与 的面积相等 的面积相等 |
(本小题满分13分)在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,底面ABCD的中心是F.
的中点,底面ABCD的中心是F.
(1) 求证: ^
^ ;
;
(2) 求证: ∥平面
∥平面 ;
;
(3) 求三棱锥 的体积。
的体积。
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
在如图所示的多面体 中,
中, 平面
平面 ,
, 平面
平面 ,
, ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
(本小题满分14分))如图,在三棱柱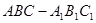 中,
中, ⊥底面
⊥底面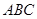 ,且△
,且△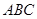 为正三角形,
为正三角形,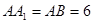 ,
,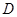 为
为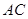 的中点.
的中点.
(1)求证:直线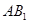 ∥平面
∥平面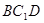 ;
;
(2)求证:平面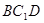 ⊥平面
⊥平面 ;
;
(3)求三棱锥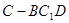 的体积.
的体积.
一个多面体的直观图及三视图如图所示,其中M ,N 分别是AF、BC 的中点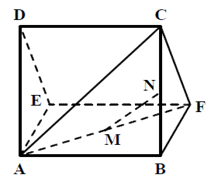
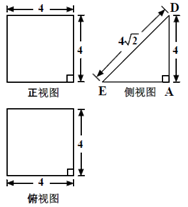
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
如图所示,一个空间几何体的正视图,侧视图,俯视图为全等的等腰直角三角形,,如果直角三角形的直角边边长都为1.
(1)画出几何体的直观图(不要求写出做图过程);
(2)求几何体的表面积和体积
如图, 为圆
为圆 的直径,点
的直径,点 .
. 在圆
在圆 上,且
上,且 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, .
.
(1)设 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
如图, 四棱柱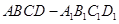 的底面ABCD是正方形, O为底面中心,
的底面ABCD是正方形, O为底面中心,  ⊥平面ABCD,
⊥平面ABCD, 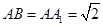 .
.
(1)证明: 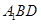 // 平面
// 平面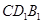 ;
;
(2)求三棱柱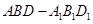 的体积.
的体积.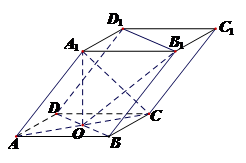
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.
如图,圆柱的轴截面 为正方形,
为正方形, 、
、 分别为上、下底面的圆心,
分别为上、下底面的圆心, 为上底面圆周上一点,已知
为上底面圆周上一点,已知 ,圆柱侧面积等于
,圆柱侧面积等于 .
.
(1)求圆柱的体积 ;
;
(2)求异面直线 与
与 所成角
所成角 的大小.
的大小.