(本小题满分12分)已知三棱锥 中,侧棱垂直于底面,点
中,侧棱垂直于底面,点 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若底面 为边长为
为边长为 的正三角形,
的正三角形, ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)如图 是图
是图 的三视图,三棱锥
的三视图,三棱锥 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
如图,圆O为三棱锥P-ABC的底面ABC的外接圆,AC是圆O的直径,PA BC,点M是线段PA的中点.
BC,点M是线段PA的中点.
(1)求证: BC PB;
PB;
(2)设PA AC,PA=AC=2,AB=1,求三棱锥P-MBC的体积;
AC,PA=AC=2,AB=1,求三棱锥P-MBC的体积;
(3)在 ABC内是否存在点N,使得MN∥平面PBC?请证明你的结论.
ABC内是否存在点N,使得MN∥平面PBC?请证明你的结论.
(本小题满分12分)如图,直三棱柱 中,
中, ,
, ,
, 、
、 分别为
分别为 和
和 上的点,且
上的点,且 .
.
(1)求证:当 时,
时, ;
;
(2)当 为何值时,三棱锥
为何值时,三棱锥 的体积最小,并求出最小体积.
的体积最小,并求出最小体积.
(本题满分 8 分)如图,正四棱柱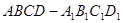 的底面边长
的底面边长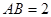 ,若异面直线
,若异面直线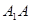 与
与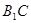 所成角的大小为
所成角的大小为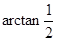 ,求正四棱柱
,求正四棱柱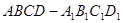 的体积.
的体积.
如图:三棱锥P-ABC中,PA^底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为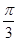 .若
.若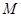 是
是 的中点,求:
的中点,求: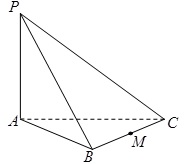
(1)三棱锥P-ABC的体积;
(2)异面直线PM与AC所成角的大小(结果用反三角函数值表示).
已知四棱锥 ,侧面
,侧面 底面
底面 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面 为菱形,且
为菱形,且 .
.
(1)求证: ;
;
(2)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
(本小题满分14分)
如图,边长为4的正方形 中,点
中,点 分别是
分别是 上的点,将
上的点,将 折起,使
折起,使 两点重合于
两点重合于 .
.
(1)求证: ;
;
(2)当 时,
时,
求四棱锥 的体积.
的体积.
(本小题13分)已知:一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱.
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大。
如图,菱形 的边长为4,
的边长为4, ,
, .将菱形
.将菱形 沿
沿
对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC
(3)求三棱锥B﹣DOM的体积.
(本小题6分)如图,已知—正三棱锥P- ABC的底面棱长AB=3,高PO=  ,求这个正三棱锥的表面积.
,求这个正三棱锥的表面积.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点, 是AC的中点,已知
是AC的中点,已知 ,
, .
.
(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥 的体积.
的体积.