如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，
是AC的中点，已知
，
．
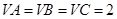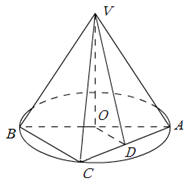
（1）求证：OD//平面VBC；
（2）求证：AC⊥平面VOD；
（3）求棱锥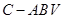
的体积．
相关试题
=1,求a
的最大值.相关知识点
推荐套卷
如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，是AC的中点，已知，．
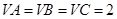（1）求证：OD//平面VBC；
（2）求证：AC⊥平面VOD；
（3）求棱锥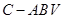的体积．
粤公网安备 44130202000953号