如图,三棱柱 中,侧棱
中,侧棱 平面
平面 ,
, 为等腰直角三角形,
为等腰直角三角形,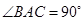 ,且
,且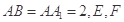 分别是
分别是 的中点.
的中点.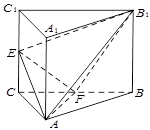
(1)求证: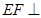 平面
平面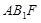 ;
;
(2)求三棱锥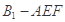 的体积.
的体积.
(3)若点 是
是 上一点,求
上一点,求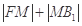 的最小值.
的最小值.
(本小题12分)如图4,四棱锥 中,底面
中,底面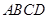 是菱形,其对角线的交点为
是菱形,其对角线的交点为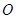 ,且
,且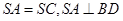 .
.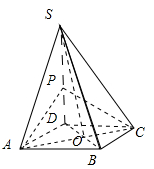
(1)求证: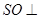 平面
平面 ;
;
(2)设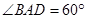 ,
,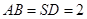 ,
,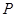 是侧棱
是侧棱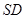 上的一点,且
上的一点,且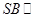 平面
平面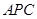 ,求三棱锥
,求三棱锥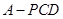 的体积.
的体积.
如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.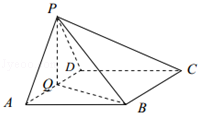
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
(本小题满分12分)在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=1,AB=4,BC=2 ,∠CBA=30°.
,∠CBA=30°.
(1)求证:AC⊥PB;
(2)当PD=2时,求此四棱锥的体积.
如图,已知圆锥的底面半径为 ,点Q为半圆弧
,点Q为半圆弧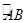 的中点,点
的中点,点 为母线
为母线 的中点.若直线
的中点.若直线 与
与 所成的角为
所成的角为 ,求此圆锥的表面积.
,求此圆锥的表面积.
已知四边形 满足
满足 ,
, ,
, 是
是 的中点,将
的中点,将 沿着
沿着 翻折成
翻折成 ,使面
,使面 面
面 ,
, 分别为
分别为
 的中点.
的中点. 

(1)求三棱锥 的体积;
的体积;
(2)证明: ∥平面
∥平面 ;
;
(3)证明:平面 平面
平面
(本小题满分14分)四棱锥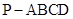 中,
中,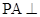 底面
底面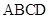 ,
,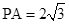 ,
,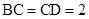 ,
,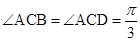 .
.
(1)求证: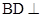 平面
平面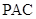 ;
;
(2)若侧棱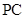 上的点
上的点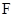 满足
满足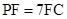 ,求三棱锥
,求三棱锥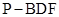 的体积.
的体积.
【原创】下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
(1)请画出四棱锥S-ABCD的直观图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA 面ABCD,E为AB中点,求三棱锥
面ABCD,E为AB中点,求三棱锥 的体积;
的体积;
(3)求点D到面SEC的距离。
(本小题满分12分)在平行六面体 中,
中, ,
, ,
, 是
是 的中点.
的中点.
(1)证明 面
面 ;
;
(2)当平面 平面
平面 ,求
,求 .
.
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(Ⅰ)当点 为
为 边的中点时,判断
边的中点时,判断 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)证明:无论点 在
在 边的何处,都有
边的何处,都有 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(本小题满分14分)如图,在直三棱柱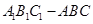 中,
中, ,
,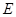 、
、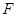 分别是
分别是 ,
, 的中点.
的中点.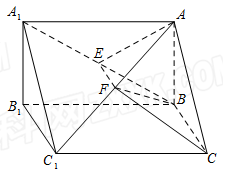
(1)求证: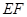 ∥平面
∥平面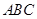 ;
;
(2)求证:平面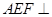 平面
平面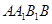 ;
;
(3)若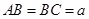 ,
,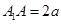 ,求三棱锥
,求三棱锥 的体积.
的体积.
已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.
(1)画出该三棱锥的直观图;
(2)求出侧视图的面积.