已知直线: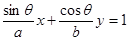 (
( 为给定的正常数,
为给定的正常数, 为参数,
为参数, )构成的集合为S,给出下列命题:
)构成的集合为S,给出下列命题:
①当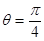 时,
时,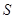 中直线的斜率为
中直线的斜率为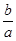 ;
;
②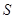 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当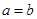 时,存在某个定点,该定点到
时,存在某个定点,该定点到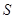 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当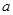 >
>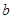 时,
时,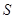 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为 ;
;
其中正确的是 (写出所有正确命题的编号).
以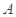 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,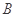 表示具有如下性质的函数
表示具有如下性质的函数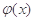 组成的集合:对于函数
组成的集合:对于函数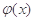 ,存在一个正数
,存在一个正数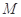 ,使得函数
,使得函数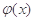 的值域包含于区间
的值域包含于区间 。例如,当
。例如,当 ,
,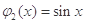 时,
时,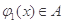 ,
,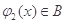 。现有如下命题:
。现有如下命题:
①设函数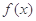 的定义域为
的定义域为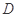 ,则“
,则“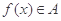 ”的充要条件是“
”的充要条件是“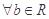 ,
, ,
,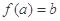 ”;
”;
②函数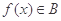 的充要条件是
的充要条件是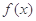 有最大值和最小值;
有最大值和最小值;
③若函数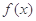 ,
,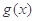 的定义域相同,且
的定义域相同,且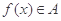 ,
,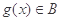 ,则
,则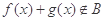
④若函数 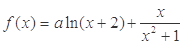 (
(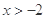 ,
, )有最大值,则
)有最大值,则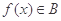 。
。
其中的真命题有__________________.(写出所有真命题的序号).
给出下列四个命题:
①命题“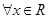 ,
, ”的否定是“
”的否定是“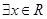 ,
, ”;
”;
②已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是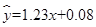 ;
;
③圆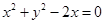 的圆心到直线
的圆心到直线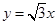 的距离是
的距离是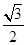 ;
;
④若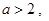 则方程
则方程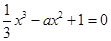 在
在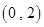 上恰好有1个根;
上恰好有1个根;
⑤对于大于1的自然数m的二次幂可以用技术进行以下方式的“分裂”: ……仿此,若
……仿此,若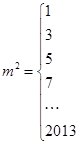 ,则m=1007;
,则m=1007;
其中真命题的序号是 .(填上所有真命题的序号)
给出下列四个命题:
①命题“ ”的否定是“
”的否定是“ ”;
”;
②“ ”是“直线
”是“直线 与直线
与直线 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆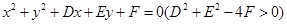 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
;
④关于 的不等式
的不等式 的解集为
的解集为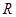 ,则
,则 .
.
其中所有真命题的序号是 .
给出下列四个命题:
①命题“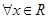 ,
, ”的否定是“
”的否定是“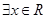 ,
,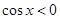 ”;
”;
②若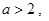 则方程
则方程 在
在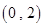 上恰好有1个根;
上恰好有1个根;
③如果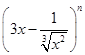 的展开式中二项式系数之和为128,则展开式中
的展开式中二项式系数之和为128,则展开式中 的系数是
的系数是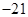 ;
;
④由直线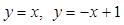 ,及x轴围成平面图形的面积为
,及x轴围成平面图形的面积为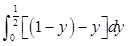 ;
;
其中真命题的序号是 .(填上所有真命题的序号)
以 表示值域为
表示值域为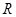 的函数组成的集合,
的函数组成的集合,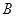 表示具有如下性质的函数
表示具有如下性质的函数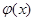 组成的集合:对于函数
组成的集合:对于函数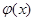 ,存在一个正数
,存在一个正数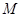 ,使得函数
,使得函数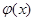 的值域包含于区间
的值域包含于区间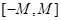 .例如,当
.例如,当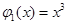 ,
,
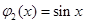 时,
时,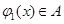 ,
,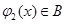 .现有如下命题:
.现有如下命题:
①设函数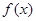 的定义域为
的定义域为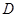 ,则“
,则“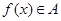 ”的充要条件是“
”的充要条件是“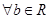 ,
, ,
,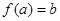 ”;
”;
②函数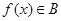 的充要条件是
的充要条件是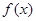 有最大值和最小值;
有最大值和最小值;
③若函数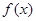 ,
,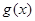 的定义域相同,且
的定义域相同,且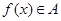 ,
, ,则
,则 ;
;
④若函数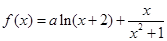 (
(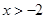 ,
,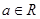 )有最大值,则
)有最大值,则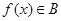 .
.
其中的真命题有 (写出所有真命题的序号).
在下列给出的命题中,所有正确命题的序号为 .
①函数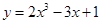 的图象关于点
的图象关于点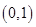 成中心对称;
成中心对称;
②对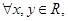 若
若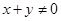 ,则
,则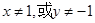 ;
;
③若实数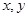 满足
满足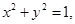 则
则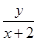 的最大值为
的最大值为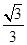 ;
;
④若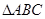 为钝角三角形,则
为钝角三角形,则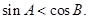
已知函数 的定义域为
的定义域为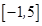 ,部分对应值如下表,
,部分对应值如下表, 的导函数
的导函数 的图象如图所示.下列关于
的图象如图所示.下列关于 的命题:
的命题:
 |
 |
0 |
4 |
5 |
 |
1 |
2 |
2 |
1 |
①函数 的极大值点为
的极大值点为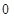 ,
, ;
;
②函数 在
在 上是减函数;
上是减函数;
③如果当 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;
④当 时,函数
时,函数 有
有 个零点。
个零点。
其中正确命题的个数有 个.
下列说法:
① “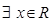 ,使
,使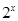 >3”的否定是“
>3”的否定是“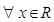 ,使
,使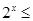 3”;
3”;
② 函数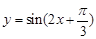 的最小正周期是
的最小正周期是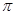 ;
;
③ “在 中,若
中,若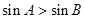 ,则
,则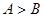 ”的逆命题是真命题;
”的逆命题是真命题;
④ “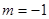 ”是“直线
”是“直线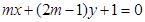 和直线
和直线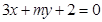 垂直”的充要条件;其中正确的说法是 (只填序号).
垂直”的充要条件;其中正确的说法是 (只填序号).
下列说法:
①“∃x∈R,2x>3”的否定是“∀x∈R,2x≤3”;
②函数y=sin 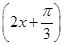 sin
sin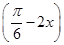 的最小正周期是π;
的最小正周期是π;
③命题“函数f(x)在x=x0处有极值,则f′(x0)=0”的否命题是真命题;
④f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,则x<0时的解析式为f(x)=-2-x.其中正确的说法是________.
定义:如果函数 在定义域内给定区间
在定义域内给定区间 上存在
上存在 ,满足
,满足 ,则称函数
,则称函数 是
是 上的“平均值函数”,
上的“平均值函数”, 是它的一个均值点.例如y=| x |是
是它的一个均值点.例如y=| x |是 上的“平均值函数”,0就是它的均值点.给出以下命题:
上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数 是
是 上的“平均值函数”.
上的“平均值函数”.
②若 是
是 上的“平均值函数”,则它的均值点x0≥
上的“平均值函数”,则它的均值点x0≥ .
.
③若函数 是
是 上的“平均值函数”,则实数m的取值范围是
上的“平均值函数”,则实数m的取值范围是 .
.
④若 是区间[a,b] (b>a≥1)上的“平均值函数”,
是区间[a,b] (b>a≥1)上的“平均值函数”, 是它的一个均值点,则
是它的一个均值点,则 .
.
其中的真命题有 .(写出所有真命题的序号)
给出下列四个结论:
①命题“ 的否定是“
的否定是“ ”;
”;
②“若 则
则 ”的逆命题为真;
”的逆命题为真;
③函数 (x
(x )有3个零点;
)有3个零点;
④对于任意实数x,有 且x>0时,
且x>0时, 则x<0时
则x<0时
其中正确结论的序号是 .(填上所有正确结论的序号)