在下列给出的命题中,所有正确命题的序号为 .
①函数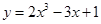 的图象关于点
的图象关于点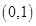 成中心对称;
成中心对称;
②对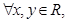 若
若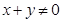 ,则
,则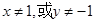 ;
;
③若实数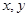 满足
满足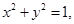 则
则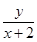 的最大值为
的最大值为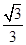 ;
;
④若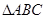 为钝角三角形,则
为钝角三角形,则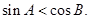
下列四个命题:
①命题“若 ,则
,则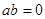 ”的否命题是“若
”的否命题是“若 ,则
,则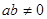 ”;
”;
②若命题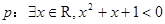 ,则
,则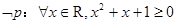 ;
;
③若命题“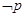 ”与命题“
”与命题“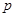 或
或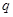 ”都是真命题,则命题
”都是真命题,则命题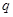 一定是真命题;
一定是真命题;
④命题“若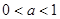 ,则
,则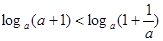 ”是真命题.
”是真命题.
其中正确命题的序号是 .(把所有正确的命题序号都填上)
给出以下四个命题:
①已知命题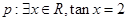 ;命题
;命题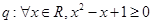 .则命题
.则命题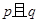 是真命题;
是真命题;
②命题“若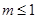 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
③命题“面积相等的三角形全等”的否命题;
④命题 的逆命题.
的逆命题.
其中正确命题的序号为___________.(把你认为正确的命题序号都填上)
定义: 表示
表示 两个数中的最大值,
两个数中的最大值, 表示
表示 两个数中的最小值。给出下列4个命题:
两个数中的最小值。给出下列4个命题:
①
 且
且 ;
;
②
 且
且 ;
;
③设函数 和
和 的公共定义域为
的公共定义域为 ,若
,若 ,
, 恒成立,则
恒成立,则 ;
;
④若函数 的图像关于直线
的图像关于直线 对称,则
对称,则 的值为
的值为 。
。
其中真命题是 。(写出所有真命题的序号)
命题“ x0∈R,使得
x0∈R,使得 +2x0+5>0”的否定是____________________.
+2x0+5>0”的否定是____________________.
在平面直角坐标系中,动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P的轨迹为曲线W,给出下列四个结论:
①曲线W关于原点对称;
②曲线W关于直线y=x对称;
③曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于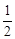 ;
;
④曲线W上的点到原点距离的最小值为
其中,所有正确结论的序号是________.
在直角坐标系内,点 实施变换
实施变换 后,对应点为
后,对应点为 ,给出以下命题:
,给出以下命题:
①圆 上任意一点实施变换
上任意一点实施变换 后,对应点的轨迹仍是圆
后,对应点的轨迹仍是圆 ;
;
②若直线 上每一点实施变换
上每一点实施变换 后,对应点的轨迹方程仍是
后,对应点的轨迹方程仍是 则
则 ;
;
③椭圆 上每一点实施变换
上每一点实施变换 后,对应点的轨迹仍是离心率不变的椭圆;
后,对应点的轨迹仍是离心率不变的椭圆;
④曲线 :
: 上每一点实施变换
上每一点实施变换 后,对应点的轨迹是曲线
后,对应点的轨迹是曲线 ,
, 是曲线
是曲线 上的任意一点,
上的任意一点, 是曲线
是曲线 上的任意一点,则
上的任意一点,则 的最小值为
的最小值为 。
。
以上正确命题的序号是 (写出全部正确命题的序号).
如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.
①不存在点D,使四面体ABCD有三个面是直角三角形
②不存在点D,使四面体ABCD是正三棱锥
③存在点D,使CD与AB垂直并且相等
④存在无数个点D,使点O在四面体ABCD的外接球面上
其中真命题的序号是
 |
已知点 是定圆
是定圆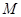 所在平面上的一定点,点
所在平面上的一定点,点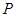 是圆
是圆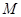 上的动点,若线段
上的动点,若线段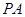 的垂直平分线交直线
的垂直平分线交直线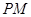 于点
于点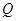 ,则点
,则点 的轨迹可能是:①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.其中正确命题的序号是_________.(填上你认为所有正确命题的序号)
的轨迹可能是:①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.其中正确命题的序号是_________.(填上你认为所有正确命题的序号)