设全集U=R,A={y|y= },B={x|y=ln(1-2x)}.
},B={x|y=ln(1-2x)}.
(1)求A∩(CUB);
(2)记命题p:x∈A,命题q:x∈B,求满足“p∧q”为假的x的取值范围.
已知命题p: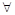 x∈[1,2],x2-a≥0;命题q:
x∈[1,2],x2-a≥0;命题q: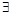 x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。
x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。
已知p:f(x)= ,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
已知 ,设命题
,设命题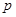 :函数
:函数 在区间
在区间 上与
上与 轴有两个不同的交点;命题
轴有两个不同的交点;命题 :
: 在区间
在区间 上有最小值.若
上有最小值.若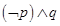 是真命题,求实数
是真命题,求实数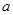 的取值范围.
的取值范围.