高中数学多面角及多面角的性质试题

设函数的导函数的图像位于轴右侧的所有对称中心从左到右依次为，O为坐标原点，则的坐标为：           ．

已知，，（1）把的图像向右平移个
单位得的图像，求的单调递增区间 （2）当与共线时，求的值

已知向量，，设函数．
（1）求函数的单调递减区间；
（2）在△ABC中，角A，B，C的对边分别为a，b，c，且满足，，求的值．

函数的部分图象如图所示，如果、，且，则等于（  ）

A．

B．

C．

D．1

已知函数的一系列对应值如下表：

 
（1）根据表格提供的数据求函数的一个解析式；
（2）根据（1）的结果，若函数周期为，当时，方程恰有两个不同的解，求实数的取值范围．

已知函数，则如下结论：
①函数的最小正周期为；
②函数在上的值域为；
③函数在上是减函数；
④函数的图象向左平移个单位得到函数的图象，
其中正确的是      （写出所有正确的序号）

已知函数在区间上的最大值为．
（Ⅰ）求常数的值;   
（Ⅱ）在中,角所对的边长分别为,若,,面积为,求边长的值．

（本题8分）已知函数．
（Ⅰ）当时，求函数的最小值和最大值;
（Ⅱ）设△ABC的对边分别为，若=，，，求的值．

已知函数
（Ⅰ）求函数y = f（x）的单调递增区间；
（Ⅱ）当x ∈ ［0，］ 时，函数 y = f（x）的最小值为 ，试确定常数a的值．

（，，为常数，，，）的图象如图所示，则的值为      ．

（本小题12分）设函数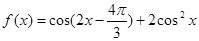
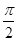（1）把函数的图像向右平移个单位，再向下平移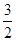个单位得到函数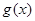的图像，求函数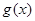在区间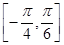上的最小值，并求出此时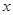的值；
（2）已知△ABC中，角A，B，C的对边分别为a，b，c．若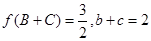．求a的最小值．

（本小题满分12分）已知函数，是的导函数．
（1）求函数的最小值及相应的值的集合；
（2）若，求的值．

已知函数（），相邻两对称轴之间的距离为．
（1）求函数的解析式；
（2）把函数的图象向右平移个单位，再纵坐标不变横坐标缩短到原来的后得到函数的图象，当 时，求函数的单调递增区间．

已知函数
（1）当时，化简的解析式并求的对称轴和对称中心；
（2）当时，求函数的值域．

已知函数.若存在，，，满足，且，则的最小值为          .